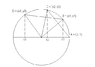
The classic development of these formulae that I've seen follows these lines:
Begin with cos(a - b). Draw a unit circle centered at O = (0, 0) with a point at A = (1, 0) and three others labeled B = (x1, y1), C = (x2, y2), and D = (x3, y3) on the circumference situated at angles b, a - b, and a radians respectively. Since the angles COA and DOB are both (a - b) then the distances CA and DB must be the same. Calculating these distances leads to the derivation of cos(a - b), which is x2.
cos(a + b) follows from cos(a - (-b)).
sin(a - b) follows from cos((π/2 - a) + b) via co-fuction identity sin(u) = cos(π/2 - u).
sin(a + b) follows from sin(a - (-b)).
There are other derivations of cos(a - b) than the one I gave above.
If this isn't clear enough, I will try to hammer out a daigram with proof.
--Elucidus