embassyhill
- 5
- 0
This is supposed to be a proof of trigonometric multiplication of complex numbers:
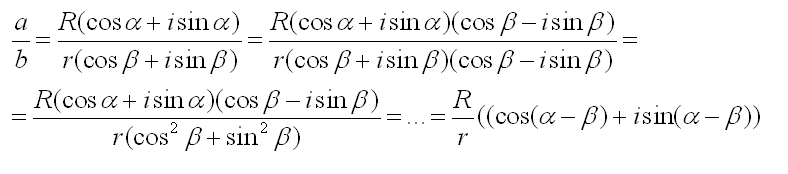
What happened at the =...= point? I understand everything up to that.
What happened at the =...= point? I understand everything up to that.