mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
I am facing some troubles understanding the proof of the following theorem.
Let $\overrightarrow{F}$ be a vector field, $\overrightarrow{F}=M\hat{\imath}+N\hat{\jmath}+P\hat{k}$, where $M,N,P$:continuous at a region $D$ ($M,N,P \in C^0(D)$) . Then a suficient and necesary condition so that the integral $\int_A^B{\overrightarrow{F}d \overrightarrow{R}}$ is independent from the path from $A$ to $B$ in $D$ is that there is a differentiable function $f$ such that $\overrightarrow{F}=\nabla f= \hat{\imath} \frac{\partial{f}}{\partial{x}}+\hat{\jmath} \frac{\partial{f}}{\partial{y}}+\hat{k} \frac{\partial{f}}{\partial{z}}$ in $D$.
In this case the value of the integral is given by:
$$\int_A^B \overrightarrow{F}d \overrightarrow{R}=f(B)-f(A)$$
The proof that I am given is the following:
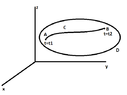
View attachment 2552
$$\overrightarrow{R}(t)=(x(t), y(t), z(t)), t_1 \leq t \leq t_2$$
$\displaystyle{f(x(t), y(t), z(t))}$
$\displaystyle{\frac{df}{dt}=\frac{\partial{f}}{\partial{x}} \frac{dx}{dt}+\frac{\partial{f}}{\partial{y}} \frac{dy}{dt}+ \frac{\partial{f}}{\partial{z}} \frac{dz}{dt}}$
$\displaystyle{\Rightarrow \frac{df}{dt}= \nabla f \cdot \frac{d \overrightarrow{R}}{dt}}$
$\displaystyle{\overrightarrow{F} \cdot d \overrightarrow{R}=\nabla f \cdot \frac{d \overrightarrow{R}}{dt} dt=\frac{df}{dt}dt=\overrightarrow{F} \cdot d \overrightarrow{R}}$
$\displaystyle{\int_A^B \overrightarrow{F} d \overrightarrow{R}=\int_{t_1}^{t_2} \frac{df}{dt} dt=f(B)-f(A)}$ $\ \ \ \ (*)$
$\overrightarrow{F}(x,y,z)=\hat{\imath} M(x,y,z)+\hat{\jmath} N(x,y,z)+\hat{k} P(x,y,z)$
We will show that: $$\frac{\partial{f}}{\partial{x}}=M, \frac{\partial{f}}{\partial{y}}=N, \frac{\partial{f}}{\partial{z}}=P$$
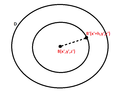
View attachment 2553
$$x=x'+t \cdot h, y=y', z=z', 0 \leq t \leq 1$$
$$\frac{f(x'+h, y', z')-f(x', y', z')}{h}=\frac{1}{h} \int_B^{B'} \overrightarrow{F} d \overrightarrow{R}=\frac{1}{h} \int_0^1 M(x'+t \cdot h, y', z') \cdot h dt= \int_0^1 M(x'+t \cdot h, y', z') dt$$
$$h \rightarrow 0$$
$$\frac{\partial{f}}{\partial{x}}=M(x,y,z)$$
In a similar way can show that
$$\frac{\partial{f}}{\partial{y}}=N(x,y,z), \frac{\partial{f}}{\partial{z}}=P(x,y,z)$$
__________________________________________________________________________
At the beginning (till the point $(*)$ ) we suppose that there is a differentiable function $f$ such that $\overrightarrow{F}=\nabla f$ and we show that the integral $\int_A^B \overrightarrow{F} d \overrightarrow{R}$ is equal to $f(B)-f(A)$. Or have I understood it wrong? (Wondering)
Then I haven't understood the proof from the point
"$\overrightarrow{F}(x,y,z)=\hat{\imath} M(x,y,z)+\hat{\jmath} N(x,y,z)+\hat{k} P(x,y,z)$
We will show that: $\frac{\partial{f}}{\partial{x}}=M, \frac{\partial{f}}{\partial{y}}=N, \frac{\partial{f}}{\partial{z}}=P$ $ \dots \dots \dots "$ (Worried)
Could you explain it to me? (Wondering)
I am facing some troubles understanding the proof of the following theorem.
Let $\overrightarrow{F}$ be a vector field, $\overrightarrow{F}=M\hat{\imath}+N\hat{\jmath}+P\hat{k}$, where $M,N,P$:continuous at a region $D$ ($M,N,P \in C^0(D)$) . Then a suficient and necesary condition so that the integral $\int_A^B{\overrightarrow{F}d \overrightarrow{R}}$ is independent from the path from $A$ to $B$ in $D$ is that there is a differentiable function $f$ such that $\overrightarrow{F}=\nabla f= \hat{\imath} \frac{\partial{f}}{\partial{x}}+\hat{\jmath} \frac{\partial{f}}{\partial{y}}+\hat{k} \frac{\partial{f}}{\partial{z}}$ in $D$.
In this case the value of the integral is given by:
$$\int_A^B \overrightarrow{F}d \overrightarrow{R}=f(B)-f(A)$$
The proof that I am given is the following:
View attachment 2552
$$\overrightarrow{R}(t)=(x(t), y(t), z(t)), t_1 \leq t \leq t_2$$
$\displaystyle{f(x(t), y(t), z(t))}$
$\displaystyle{\frac{df}{dt}=\frac{\partial{f}}{\partial{x}} \frac{dx}{dt}+\frac{\partial{f}}{\partial{y}} \frac{dy}{dt}+ \frac{\partial{f}}{\partial{z}} \frac{dz}{dt}}$
$\displaystyle{\Rightarrow \frac{df}{dt}= \nabla f \cdot \frac{d \overrightarrow{R}}{dt}}$
$\displaystyle{\overrightarrow{F} \cdot d \overrightarrow{R}=\nabla f \cdot \frac{d \overrightarrow{R}}{dt} dt=\frac{df}{dt}dt=\overrightarrow{F} \cdot d \overrightarrow{R}}$
$\displaystyle{\int_A^B \overrightarrow{F} d \overrightarrow{R}=\int_{t_1}^{t_2} \frac{df}{dt} dt=f(B)-f(A)}$ $\ \ \ \ (*)$
$\overrightarrow{F}(x,y,z)=\hat{\imath} M(x,y,z)+\hat{\jmath} N(x,y,z)+\hat{k} P(x,y,z)$
We will show that: $$\frac{\partial{f}}{\partial{x}}=M, \frac{\partial{f}}{\partial{y}}=N, \frac{\partial{f}}{\partial{z}}=P$$
View attachment 2553
$$x=x'+t \cdot h, y=y', z=z', 0 \leq t \leq 1$$
$$\frac{f(x'+h, y', z')-f(x', y', z')}{h}=\frac{1}{h} \int_B^{B'} \overrightarrow{F} d \overrightarrow{R}=\frac{1}{h} \int_0^1 M(x'+t \cdot h, y', z') \cdot h dt= \int_0^1 M(x'+t \cdot h, y', z') dt$$
$$h \rightarrow 0$$
$$\frac{\partial{f}}{\partial{x}}=M(x,y,z)$$
In a similar way can show that
$$\frac{\partial{f}}{\partial{y}}=N(x,y,z), \frac{\partial{f}}{\partial{z}}=P(x,y,z)$$
__________________________________________________________________________
At the beginning (till the point $(*)$ ) we suppose that there is a differentiable function $f$ such that $\overrightarrow{F}=\nabla f$ and we show that the integral $\int_A^B \overrightarrow{F} d \overrightarrow{R}$ is equal to $f(B)-f(A)$. Or have I understood it wrong? (Wondering)
Then I haven't understood the proof from the point
"$\overrightarrow{F}(x,y,z)=\hat{\imath} M(x,y,z)+\hat{\jmath} N(x,y,z)+\hat{k} P(x,y,z)$
We will show that: $\frac{\partial{f}}{\partial{x}}=M, \frac{\partial{f}}{\partial{y}}=N, \frac{\partial{f}}{\partial{z}}=P$ $ \dots \dots \dots "$ (Worried)
Could you explain it to me? (Wondering)
Attachments
Last edited by a moderator: