mathstudent88
- 25
- 0
Incidence Postualte I-1 holes for the Poincare Model: Every two points of E lie on exactly one L-Line.
Prove: Given any two points P and Q inside the unit circle C, there exists a unique L-line l containing them. (this will require the use of analytic geometry.)
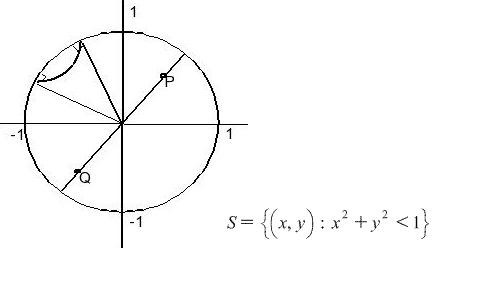
L-lines:arcs of circles perpendicular to the unit circle in S and the diameter of S.
How would i solve this? I know that i need to prove and P,Q are not equal to the orgin and that either one is at the orgin, but how?
Thanks for the help!
Prove: Given any two points P and Q inside the unit circle C, there exists a unique L-line l containing them. (this will require the use of analytic geometry.)
L-lines:arcs of circles perpendicular to the unit circle in S and the diameter of S.
How would i solve this? I know that i need to prove and P,Q are not equal to the orgin and that either one is at the orgin, but how?
Thanks for the help!