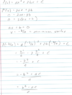Prove that f(x)>=0 for all x in R iff b^2-ac=<0

  • Thread starter Robb
  • Start date
In summary, the conversation discusses finding the minimum value of a function and using the hypothesis of a>0 to show that the function is positive. The expression ##b^2-ac \leq 0## is used to show that the minimum value is greater than or equal to 0. It is also mentioned that the second derivative test for extrema can be used to show that the function is positive.
  • #1
Robb
225
8

Homework Statement


upload_2019-1-22_16-53-8.png


Homework Equations

The Attempt at a Solution


This is where I'm at and I'm not sure what my next step is. Any help would be much appreciated!
upload_2019-1-22_16-56-41.png
 

Attachments

  • upload_2019-1-22_16-53-8.png
    upload_2019-1-22_16-53-8.png
    6.3 KB · Views: 595
  • upload_2019-1-22_16-56-41.png
    upload_2019-1-22_16-56-41.png
    24.7 KB · Views: 629
Physics news on Phys.org
  • #2
Robb said:

Homework Statement


View attachment 237693

Homework Equations

The Attempt at a Solution


This is where I'm at and I'm not sure what my next step is. Any help would be much appreciated!
View attachment 237695

Great work so far! You made a sign mistake at the last equality though.

You want that ##f(x) \geq 0## for all ##x \in \mathbb{R}##, or equivalently (why??) ##\min f = \frac{-b^2 +ac}{a} \geq 0##. Can you proceed? Note that the hypothesis ##a>0## is essential to proceed.
 
  • #3
This is where I'm not sure. I tried setting min f = (-b^2+ac)/a and solving for x but I'm not sure if that tells me anything and it doesn't relate to the hypothesis. I guess I'm unsure of how to use the hypothesis.
 
  • #4
Robb said:
This is where I'm not sure. I tried setting min f = (-b^2+ac)/a and solving for x but I'm not sure if that tells me anything and it doesn't relate to the hypothesis. I guess I'm unsure of how to use the hypothesis.

That expression doesn't depend on ##x##...

It really is one line to get the right answer from here.
 
  • #5
Does it have to do with divisibility of a, which must be greater that zero?
 
  • #6
Robb said:
Does it have to do with divisibility of a, which must be greater that zero?

Yes, certainly.

When is the following statement true?

##ax \geq 0 \iff x \geq 0##
 
  • #7
for all x in R?
 
  • #8
Robb said:
for all x in R?

I forgot to mention that ##x \in \mathbb{R}## is fixed. I want a condition for ##a##.
 
  • #9
(a) must be greater than zero but that's a given
 
  • #10
Robb said:
(a) must be greater than zero but that's a given

Yes, indeed. Apply this and you will be done (in fact, you have to apply it to ##1/a## instead of ##a##)
 
  • #11
How does b^2-ac =< 0 tell us that f(x) >= 0?
 
  • #12
Robb said:
How does b^2-ac =< 0 tell us that f(x) >= 0?

##b^2 - ac \leq 0 \implies \frac{ac -b^2}{a} \geq 0##

Since ##\frac{ac -b^2}{a} = \min f##, we know that ##\min f \geq 0##. It is now obvious that ##f \geq 0##, as ##f \geq \min f \geq 0##
 
  • #13
NOW I GET IT! I was looking at min f as f' min. I assume I could also apply the second derivative test for extrema? So, f" = 2a, and we know a>0, hence f is positive?
 

FAQ: Prove that f(x)>=0 for all x in R iff b^2-ac=<0

What does the statement "f(x)>=0 for all x in R" mean?

The statement means that the function f(x) always has a non-negative value for any input value x from the set of real numbers.

What is the significance of b^2-ac in the given statement?

b^2-ac is the discriminant of a quadratic equation, which determines the nature of the roots of the equation. In this case, if b^2-ac is less than or equal to zero, the quadratic equation has either two real roots or no real roots, which is necessary for f(x) to be non-negative for all x in R.

How can we prove that f(x)>=0 for all x in R?

To prove that f(x)>=0 for all x in R, we need to show that the discriminant b^2-ac is less than or equal to zero for any real values of a, b, and c in the quadratic equation. This can be done by using the quadratic formula or by completing the square.

Can we use any other method to prove the given statement?

Yes, there are other methods to prove that f(x)>=0 for all x in R. For example, we can use the properties of a quadratic function, such as its vertex, to show that the function always has a non-negative value for any input x in the set of real numbers.

What is the practical application of proving that f(x)>=0 for all x in R?

The practical application of this proof is that it ensures the reliability and validity of the quadratic function in various mathematical and scientific applications. It also helps in solving optimization problems and in determining the nature of solutions to real-world problems represented by quadratic equations.

Similar threads

Proving Irregularity of {(x, y, z) within R^3 : x^2 + y^2 - z^2 = 0}
Replies
14
Views
2K
Prove that the limit of |x|/x at x=0 DNE
Replies
9
Views
2K
Prove if ##x<0## and ##y<z## then ##xy>xz## (Rudin)
Replies
2
Views
1K
f(x) = 2x+1, proving that it is continuous when p = 1 with 𝛿 and ε
Replies
7
Views
878
Let A={(x,y):x>0,x^2>y>0}. Prove for all lines through (0,0)
Replies
3
Views
1K
If A is dense in [0,1] and f(x) = 0, x in A, prove ∫fdx = 0.
Replies
2
Views
2K
Show that f such that f(x+cy)=f(x)+cf(y) is continuous
Replies
17
Views
2K
Proving Limit as x Approaches 0 for f(x)/x is 1?
Replies
7
Views
1K
T is cyclic iff there are finitely many T-invariant subspace
Replies
4
Views
3K
Show function series involving arctan is not differentiable at x=0
Replies
26
Views
2K

Hot Threads

Recent Insights

Back
Top