Proving Kirchoff's Laws algebraically

[shyguy79]

Homework Statement

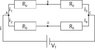
From the attached file using Kirchoff's laws prove that V AB = V AD and that i1 = i/2

Homework Equations

V1 + V2 + V3 +... Vn = 0 (The sum of the voltage applied and dropped across the components is zero.
i1 + i2 = i3 (The sum of the branch currents is equal to the total current)

The Attempt at a Solution

I thought I was ok with algebraic manipulation but this has stumped me :-( any pointers would be appreciated as always!

 

[vela]

What did you get when you tried to apply Kirchoff's laws to the circuit?

 

[shyguy79]

Hi, as there are no figures given it looks like I'm expected to do prove everything using algebra...

I've calculated hypothetic values - say V = 12v, R total = 16Ω and i total = 0.75A and everything seems to add up but I'm afraid my algebra manipulation skills are somewhat limited.

For example I've tried that if: V ab = V ad and i1 = i - i2 and i2 = i -i1 (Kirchoffs 2nd Law) then i1 R0 = i2 R0 but don't know where to go now

 

[vela]

You can't assume V_AB=V_AD because that's what you're trying to prove.

Applying KCL to node A gives you $i = i_1 + i_2$. I'm assuming all currents are flowing left to right. What do you get if you apply it to nodes B, C, and D?

 

[shyguy79]

B: i3 = i1
C: i = i3 + i4
D: i4 = i2

 

[vela]

Great! So we can eliminate i₃ and i₄ because we know they're equal to i₁ and i₂ respectively, and the equation for node C tells us the same thing as the equation for node A.

Now apply KVL to the loop ABCDA. What do you get?

 

[shyguy79]

VT - i1R0 - i1R0 - i2R0 - i2R0 = 0
VT = VAB + VBC + VDC + VAD
VT = R0 (i1+i1+i2+i2)
VT = R0 (2i1 + 2i2)

But I don't understand how V AB can be described as V AD

or even

VT = VAB + VBC + VDC + VAD

 

[vela]

VT - i1R0 - i1R0 - i2R0 - i2R0 = 0

This isn't quite right. Across the four resistors, Ohm's Law tells us the potential differences are

V_AB=i₁R₀
V_BC=i₁R₀
V_AD=i₂R₀
V_DC=i₂R₀

where the higher potential is at the left end of each resistor (where the current enters). So starting at A and going clockwise around the loop, we first encounter a voltage drop V_AB and then another drop V_BC, but going from C to D, the potential increases by V_DC because we are going from right to left, and again from D to A by V_AD. So KVL gives us

- V_AB - V_BC + V_DC + V_AD = 0

Note that V_T doesn't enter into the picture because the battery is not part of the loop ABCDA. So plugging in the values above, you get

-i₁R₀-i₁R₀+i₂R₀-i₂R₀=0

 

[shyguy79]

Oh, I see! So the direction of flow has a direct effect on the sign of the variable! Cool, there are a few more questions in this assignment but I think I understand.

Thank you for all your help!