Pulley and Work Energy problems

[Homakruz]

Well, I took a Physics midterm this morning, I had a bit of trouble with a few of the questions and was hoping I could get some help here.
I did what I thought to be right, but as I really only started picking up physics concepts just recently, I am a bit weary on if I actually computed them correctly. I am just hoping someone can check my work as I don't have an answer key.

Hopefully there is no problem with having multiple questions on one topic.
One last thing, I am rewriting these questions from memory, so if something doesn't make much sense tell me and I will try and fix it.


Problem #1:
A .5kg ball is spun around a loop on a vertical plane by a 1.45m long massless string.

If the string tension is 15N, What is the speed of the mass when it is at the top of the loop(90 degrees)?

Relevant variables:
$$m = .5kg$$ || $$r = 1.45m$$ || $$T = 15N$$ || $$\theta = 90$$

Relevant equations:
Newton's Second Law
Centripetal Acceleration

Solution Attempt:

$$F = ma$$

$$T - W = ma$$
$$T - mg = \frac{mv^2}{r}$$
$$v^2 = \frac{r(T-mg)}{m}$$

$$v = \sqrt{ r(T-mg)/m }$$

$$v = \sqrt{ 1.45( 15 - 4.9 )/ .5 }$$

$$v = 5.4 m/s$$

On this on I am just a little unsure of, I feel like I am forgeting an force somewhere in the problem.
I just want to know if I went about this one correctly.


Problem #3:
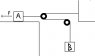
This one uses the attached figure, just to give you a visual representation of what I am explaining.
Again I am completely clueless on whether or not I subbed in the right equations here.

Box A is pulled on a frictionless surface by a force of 120N in the direction of the vector in the picture.
Both Box A and B weight 7 kg.

What is the tension in the rope holding block B?

Relevant variables:
$$m_a = m_b = 7kg$$||$$F_p = 120N$$||$$a_b = 2a_a$$

Relevant equations:
Newton's Second Law

Solution Attempt:

=> Block B:

$$F = ma$$

$$T - w = m_ba_b$$
$$T = m_ba_b + m_bg$$
$$T = m_b(a_b + g)$$

=> Block A:

$$F = ma$$

$$F_p - 2T = m_aa_a$$

I used 2T here as a part of the force because of the pulley separating the ropes into 2 equal tension parts.
I don't know if I was supposed to use this or not, but it just makes sense to do so for me.

*Subbing in $$T$$ from Block B equation.

$$F - 2m_b(a_b + g) = m_aa_a$$
$$F - 2m_ba_b - 2m_bg = m_aa_a$$
$$F - 2m_bg = m_aa_a + 2m_ba_b$$

*Subbing in $$2a_a$$ for $$a_b$$

$$F - 2m_bg = m_aa_a + 4m_ba_a$$
$$F - 2m_bg = a_a(4m_b + m_a)$$
$$a_a = \frac{F - 2m_bg}{4m_b + m_a}$$
$$a_a = \frac{120 - 2(7)(9.8)}{35}$$

$$a_a = -.49 m/s$$
$$a_b = -.98 m/s$$

*Going back to Block B equation

$$T = 7( -.98 + 9.8 )$$
$$T = 62 N$$


Anyways, any help on these 3 problems would be much appreciated, especially on the last one.
Thanks in advance!

*One more on a post down, I couldn't fit it on this post.*

 

[Homakruz]

Problem #4:
This one is giving me the most trouble of all of them. I have no idea on how to solve it the correct way as my book is a bit obscure on these problems.

A boy pushes a 12 kg sled up a 37 degree slope that is 2m high and has a kinetic friction value of .12.
He pushes with a power of 145N parallel to the slope.
What is the sled's speed when he reaches the top?

Relevant variables:
$$m = 12kg$$||$$h = 2m$$||$$\theta = 37$$||$$u_k = .12$$||$$F_p = 145N$$||$$v_i = 0m/s$$

Relevant equations:
Work Kinetic Energy Theorem?
Energy Conservation?
Kinematics?

Solution Attempt(Using Work-Energy):

$$\Delta(r) => \sin(37) = 2m/L => \Delta(r) = 3.32m$$

$$W_p = \Delta(r)(145N) = 481J$$
$$W_g = -\sin(37)(g)(12kg)(2m) = -142J$$
$$W_f = -(u_k)(12kg)(g)\Delta(r) = -47J$$
$$W_n = W_p + W_g + W_f = 292J$$

$$W_n = \Delta(K)$$
$$W_n = (1/2)mv^2 - 0$$

$$v = \sqrt{ \frac{2W_n}{m} }$$
$$v = 6.98 m/s$$

 

[Delphi51]

#1. At the top of the loop, W and T are both downward so W+T = mv²/R
Looks like that is the only error.
#3 - diagram not approved yet. Faster if you upload to a site like photobucket.com and put a link here.
#4. I'm getting a slightly different answer:
482 = mgh + Ff*L + ½mv²
482 = 12g2 + u*mg*cos(37)*L + ½mv²
482 = 235.4 + .12*12g*cos(37)*3.32 + ½mv²
482 = 235.4 + 37.5 + ½mv²
209.1 = ½*12v²
v = 5.9 m/s

 

[Homakruz]

I see what I did now on one, I just reread my book and I think I got it mixed up with a different explanation.

Here's the image for 2, it's a little simple but, the best I can do with paint.
http://img682.imageshack.us/img682/5121/pullypic.png

And for 3, I can understand the work done by gravity doesn't involve the angle of the slope but the work done by friction is a bit confusing. In my book it, doesn't really explain more so that it just has like pictures for it.
It shows if a force is moving opposite of the direction of travel then the force is F*L*cos(180).
You factored in the angle here but it is working parallel to the slope just in the opposite direction of the push. Why must you factor the angle in here if it isn't factored in during the work done by push?

Thanks for the help.

 

[Delphi51]

work against friction
Ff*L
u*mg*cos(37)*L
Here the normal force is mg*cos(37). The friction force is u times that, and the work is the force times the distance L that the force pushes the block through. The force and the distance must be in the same direction, so there has to be a cos(37) in there.

 

[Delphi51]

I think your pulley solution is all correct.

 

[Homakruz]

I see the error in my assumption now.

I totally forgot about the angle factor for the normal force. I assumed you were using the cos() factor for the direction of which the force of the kinetic friction was working against the sled.

Your explanations have clear a lot of things up. Thanks so much for the help.