SUMMARY
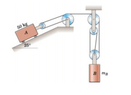
The discussion focuses on calculating the mass that balances a pulley system, specifically addressing the forces involved and the importance of free body diagrams. The force exerted by mass A is calculated as FA = sin(25°) * 50 * 9.82, resulting in 208.5 N. Participants emphasize the need to understand tension in the rope, noting that it may vary and should be symbolically represented before substituting numerical values. The advice to work symbolically helps streamline calculations and avoid unnecessary arithmetic.
PREREQUISITES
- Understanding of basic physics concepts, particularly forces and tension.
- Familiarity with free body diagrams and their application in mechanics.
- Knowledge of trigonometric functions, specifically sine, in force calculations.
- Ability to manipulate algebraic expressions symbolically before numerical evaluation.
NEXT STEPS
- Study the principles of free body diagrams in physics.
- Learn about tension in ropes and how it varies in different pulley configurations.
- Explore trigonometric functions and their applications in physics problems.
- Practice solving problems symbolically to enhance calculation efficiency.
USEFUL FOR
Students studying physics, particularly those focusing on mechanics, as well as educators and anyone interested in mastering pulley systems and force analysis.