FeelTheFire
- 8
- 0
Homework Statement
Hey guys I'm really having problems understanding this despite looking at the solution, which is fully laid out here: http://iweb.tntech.edu/murdock/books/v1chap4.pdf
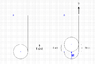
I know that m2 moves twice the distance that m1 moves. I have tried looking at each rope as a length that doesn't change made up of intervals that do change. I keep hitting a wall trying to come to the conclusion that 2a1 = a2.
I am doing pretty good understanding net forces, but this absolutely throws me for a loop. Any insight would be terrific.