Pulling a Cylinder: Understanding x, y & theta Relations

[LCSphysicist]

Homework Statement

All below

Relevant Equations

All below

Basically, the problem is pretty easy if the constraints are understood, and this is my problem.

I am trying to figure out some relation between x, y, and theta. I don't know if seeing by this way is the better attempt.

 

[haruspex]

It is unclear how you are defining x and y.
Seems to me there are three linear motions of interest. The constant that relates them is the length of the string. Write an equation to represent that.
There is also the angular motion of the cylinder, which relates to them through a second equation.

 

[ehild]

Homework Statement:: All below
Relevant Equations:: All below

View attachment 264924View attachment 264925
Basically, the problem is pretty easy if the constraints are understood, and this is my problem.
View attachment 264928I am trying to figure out some relation between x, y, and theta. I don't know if seeing by this way is the better attempt.

View attachment 264928I am trying to figure out some relation between x, y, and theta. I don't know if seeing by this way is the better attempt.

Is x is the position of the centre of the disk and y is the position of the small mass?
Take into consideration that the disk rolls on the piece of string, connected to m, but the string is also accelerating. Use the rolling condition for the motion of the disk

 

[Delta2]

I can see 4 equations with 4 unknowns (the accelerations of point mass m and center of mass of cylinder, the angular acceleration $\alpha$ of cylinder and the tension $T_m$ in front of point mass m)
One equation is the kinematic equation that relates $a_m,a_{CM}, \alpha$. In my opinion it is $$a_m=a_{CM}+\alpha r$$
Second equation and Third equation are Newton's 2nd law for the CM of cylinder and point mass m.
Fourth equation is the torque balance on the cylinder $T_{total}=I_{CM}\alpha$

I don't think you can solve the problem just by the kinematic equation as you mention in the OP.

 

[Lnewqban]

Note that the value of mass m (which only moves linearly) equals the value of the mass of the solid cylinder (which simultaneously rotates and moves linearly).
Now, imagine what would tend to happen in these two extreme conditions:

1) The value of mass m is so much bigger than the value of the mass of the solid cylinder, that you could consider the location of mass m to be an anchoring point for the string on the table.

1) The value of mass of the solid cylinder is so much bigger than the value of the mass m, that you could consider the acceleration and location of mass m irrelevant (but friction between string and cylinder still exist).

 

[LCSphysicist]

Hi you all, reviewing this problem and with a little of formalism, i solved it.
Thank you.
XYZ normal, counterclock positive
-T1 = mx''
(T1 - T)R = I*theta''
T + Ta = m*A
theta''*R = X'' - A

I got x'' = -T/4m ;) the answer

 

[LCSphysicist]

I can see 4 equations with 4 unknowns (the accelerations of point mass m and center of mass of cylinder, the angular acceleration $\alpha$ of cylinder and the tension $T_m$ in front of point mass m)
One equation is the kinematic equation that relates $a_m,a_{CM}, \alpha$. In my opinion it is $$a_m=a_{CM}+\alpha r$$
Second equation and Third equation are Newton's 2nd law for the CM of cylinder and point mass m.
Fourth equation is the torque balance on the cylinder $T_{total}=I_{CM}\alpha$

I don't think you can solve the problem just by the kinematic equation as you mention in the OP.

Hey, could you expand your method of solving? My method was correct, but a little tiring.
I see your constraints, what are the directions you adopt?
I found
ar = acm + am
i am not sure about the signals, actually who see my questions,can see that this is about 90% the responsible by the problem i have in exercises

 

[Delta2]

Hey, could you expand your method of solving? My method was correct, but a little tiring.
I see your constraints, what are the directions you adopt?
I found
ar = acm + am
i am not sure about the signals, actually who see my questions,can see that this is about 90% the responsible by the problem i have in exercises

My method of solving is basically what you did at post #6. You can take the positive x-direction towards right and for the rotation counterclockwise.
Yes you are right with this sign conventions the correct kinematic equation is $\alpha r=a_{cm}+a_{m}$.

 

[haruspex]

Hey, could you expand your method of solving? My method was correct, but a little tiring.
I see your constraints, what are the directions you adopt?
I found
ar = acm + am
i am not sure about the signals, actually who see my questions,can see that this is about 90% the responsible by the problem i have in exercises

Signs must be the biggest single cause of errors. Generally I recommend sticking to standard conventions like up, to the right and anticlockwise are positive, but when it is clear that a particular variable will turn out negative under that arrangement it can be less confusing to adopt a convention that makes each variable positive.
Whatever you choose, write it down!

In the present case, with the orthodox convention, and writing a for the particle's acceleration, we can anticipate that a will turn out negative:
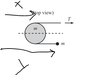
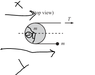
Torques about cylinder’s centre: $-(T+ma)r=\frac 12 mr^2\alpha$.
Straight away that looks weird. Why T+ma?
Since particle m accelerates at a to the right there must be a right-positive force ma acting on it. Therefore there is a right-positive force -ma acting on the bottom of the diagram of the cylinder. This exerts an anticlockwise-positive torque -mar on the cylinder. Since T exerts an anticlockwise-positive torque -Tr, the sum is -(T+ma)r.

The rightward acceleration of the cylinder is $a-r\alpha$. Again, we can predict the rotation will be clockwise, so $\alpha$ will be negative.
So for the linear acceleration of the system, $T=ma+m(a-r\alpha)$.
These lead to $a=-\frac T{4m}$.

With the "positive variables" convention, it is all the same but flipping the signs of a and $\alpha$.

So how to check that your signs are right?
One test is to consider how the result changes as a certain variable increases or decreases in magnitude. You can apply this to each equation.