Quantum Anti-Zeno Effect and Decay Rates

[Aakash Sunkari]

Hey everyone,

I have a question about how "viable" the Quantum Anti-Zeno Effect (AZE) is at lowering decay rates in radioactive nuclei. We know that the AZE can, in fact, reduce the half life of radioactive isotopes, but there seems to be a barrier to that.

AZE states that decay can be accelerated by frequent observations. Of course, in a decaying nucleus, we can "shoot" photons at it. But here's where the problem begins.

If the measurements were infrequent you could implement such a scheme in a fairly straightforward fashion. However, because the measurements must be frequent, then they also have to be short in time. The issue then becomes that a pulse cannot be arbitrarily short in time and arbitrarily specially narrow because of the time-energy uncertainty relation as shown here:

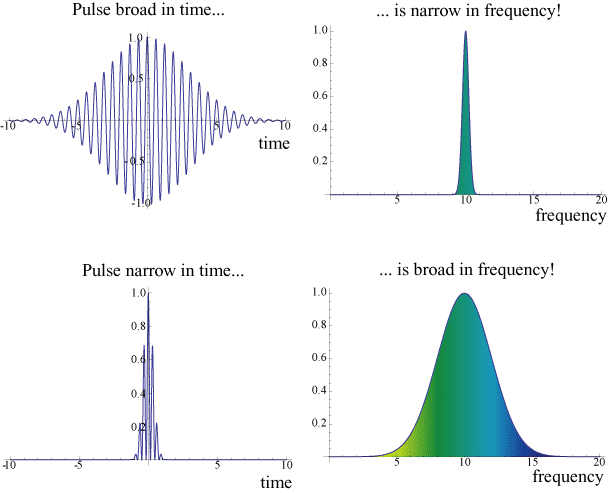
Therefore by trying to interrogate the system very quickly, you must let it interact with pulses that are very broad in energy, and which hence can perturb the system in such a fashion (e.g. coupling to other decay channels) that the net effect is an increase in the rate of decay.

My question is, how realistic is it that shooting photons can increase the decay rate of an isotope? If it is realistic, by how much? (Is there an equation for this?)

If shooting photons is an unrealistic method for frequent observation, what would be a more realistic method?

 

[mfb]

The energy scale of the decay is MeV, you would probably need MeV photons - but then you might directly induce the decays with the photons.