I Quantum Entanglement with Public Variables

[mplummer]

TL;DR Summary

Here is a thought expirment that appears to meet the observed results of entanglement

For a thought experiment, if you defined:

An electron's "state" can be in 16 states measured as increments of 45 "degrees" starting at 22.5 (modulus 360)

An entangled electron (e') simply gets aligned 180 degrees away from (e)

A "measurement" M(n) at n degrees simply adds n degrees

"Spin" is measured as 0<=e<180 then UP else DOWN

Then you would fit the observed measurements of Zero, 0.75 and 0.75 at ZERO, 120 and 240 degrees giving you the same spin 50% of the time.

 

[PeroK]

Summary:: Here is a function that appears to meet the observed results of entanglement

If you defined:

An electron's angular momentum can be in 16 states measured as increments of 45 "degrees" starting at 22.5 (modulus 360)

What am I missing?

Angular momentum is three-dimesional, so how do these states relate to the x-y-z components of spin angular momentum?

 

[Vanadium 50]

What am I missing?

Where is the quantum mechanics? You seem to think the electron possesses an exact direction in which its spin points.

You have this at A-level (graduate level). Have you taken any QM courses?

 

[mplummer]

Angular momentum is three-dimesional, so how do these states relate to the x-y-z components of spin angular momentum?

This was just a simplification to show a function that can take predetermined inputs and result in 50% same spin at the 3 angles. It can be adapted to 3 dimensions.

 

[PeroK]

This was just a simplification to show a function that can take predetermined inputs and result in 50% same spin at the 3 angles.

We all know that. It's the limitation of Bell's Theorem that is the problem for local hidden variables:

https://en.wikipedia.org/wiki/Bell's_theorem

 

[mplummer]

Where is the quantum mechanics? You seem to think the electron possesses an exact direction in which its spin points.

This was just a thought experiment to show a "state" an electron could be in, and a function that could generate a 50% same spin outcome based on that state.

 

[Nugatory]

What am I missing?

You aren’t missing anything yet. The interesting bit will happen when you take the next step, which is to see whether this simulation can violate Bell’s inequality. You will find that it cannot, whereas entangled pairs do.

 

[DrChinese]

It is not clear from this premise how you are getting UP/DOWN:

"Spin" is measured as 0<=e<180 then UP else DOWN"4

1. Because this is falsified by experiment on electrons with known spin. Electrons (for example your e or your e') with an original spin of 22.5 degrees will NOT produce a fixed outcome at other angles. They follow a cos^2(theta/2) rule, where theta=[the difference between the original spin and the observed angle]. I don't see this represented in your chart anywhere. For example: if original e=22.5, then when measured at 142.5: it will have the same spin as it originally had 25% of the time. So when you do the observation on each pair of those electrons, the outcomes follow Product State statistics, and won't match your chart.

2. It is true that actual entangled electron pairs will produce a fixed outcome (in the sense of their relative outcomes are opposite) when measured at the same angles (your O1, O2, O3 as I read your chart). They follow Entangled State statistics, which are different than Product State statistics. That being 0 (zero) in every case, because they never match at the same angle setting.

The point is: you are attempting to mix Product State outcomes with Entangled State outcomes. Now, I realize that at some level you are trying to say that we don't know which of the 16 cases you present will actually occur, and the observations you chose to consider (O1/O2/O3) are cherry picked as others have already mentioned. So...

3. I can assure you that if you measure a pair of entangled electrons at the SAME angle for both - regardless of that angle - the results will never match (and will not be 50% as you show on the right side of the chart). In other words: O1 both=O2 both=O3 both=0. And if you measure a pair of electrons with known and opposite spins at the same angle for both (as you show on the left side of your chart), their spins will match following a function that considers both the input spins and the angle you chose to measure they at. That number would average (of the course of your chart, repeated enough times): O1 both=0; O2 both=.375; O3=.375. And would never be 50%.

(All of the above assume that M(x) means adding x to the Original angle for the e particle, which appears to be what you are doing.)

 

[mplummer]

Thank you for the detailed response, much appreciated.

There were 3 "tests" whereby the measurements of Bob (e') were always at 0 degrees and the measurements of Alice were at 0, 120 and 240 degrees respectively (for the three tests O1, O2, and O3).

For test O1 (zero degrees for both) the spin was always opposite (as you state above). The second and third tests saw the same spin 75% of the time.

I was trying to show that, even though we don't know the spin of an electron, let's assume it could be in one of 16 states and let us show all permutations of those states and what the result would be in the table above.

One could create a PDF out of those states, but I needed the observation value (degrees) to go into the underlying function and not the probability field.

 

[PeroK]

I was trying to show that, even though we don't know the spin of an electron, let's assume it could be in one of 16 states and let us show all permutations of those states and what the result would be in the table above.

None of that has anything to do with quantum mechanics. Here are the specific spin statistics from QM calculations that you would need to recreate using local variables:

https://en.wikipedia.org/wiki/Bell'...hanical_predictions_violate_CHSH_inequalities

Or, see (for example): Modern Quantum Mechanics, JJ Sakurai, section 3.9.

 

[DrChinese]

There were 3 "tests" whereby the measurements of Bob (e') were always at 0 degrees and the measurements of Alice were at 0, 120 and 240 degrees respectively (for the three tests O1, O2, and O3).

OK, upon re-reading, I can see how you got to this - and also why I read it a different way. So here are a few comments.

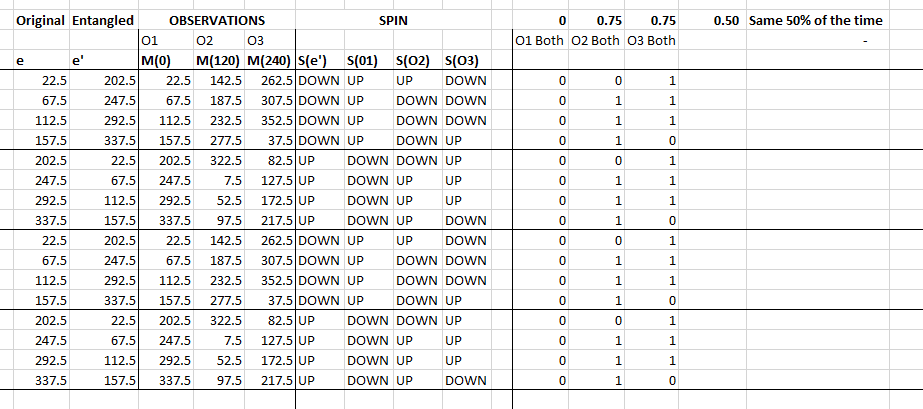
a. My 1st and 2nd comments I made (post #8) about mixing the Product state situation and the Entangled state situation still apply. If you have known spin values (left side), you don't get the outcomes you show (on the right side). For example: if you take your first line, where e=22.5 and e'=202.5 and perform tests on e' at 0 degrees and e at 120 degrees (your O2 case): The actual outcome will be closer to .75 rather than the 0 you show. For the O3 case, the actual outcome will be closer to .75 rather than the 1 you show.

My point here is that your premise ["Spin" is measured as 0<=e<180 then UP else DOWN"] is falsified before you ever get started. So it makes it difficult to consider any conclusion which includes that premise.b. However, we can get past that obstacle. First we need to modify your chart a bit. Normally, what is your O1 case is called the "Perfect Correlations" case. You need this to be true, and it is in your scenario. So let's skip that for now, and consider only your O2 and O3 cases. By your reasoning, they produce an average of .75. That's correct, that matches the Entangled State statistics when theta (the difference in angle settings) is 120 degrees. For entangled electrons, the formula is:

Entangled State Formula:
MatchRate=1-(cos^2(theta/2))
For 120 degrees:
1-(cos(120/2))^2 = 1-cos(60)^2 = 1-((.5)^2) = 1-.25=.75

But now let's add a new case, we'll call that O4. In the O4 case, you measure e at 120 degrees (like your O2 case) but you measure e' at 240 degrees (instead of 0 degrees). Since this is 120 degrees apart, your model should also yield a value of .75 just like the O2 and O3 cases (which also have 120 degrees difference). But if you actually run it out on your model (using your same algorithm), you will see that the value is closer to .50. This demonstrates that your model is not internally consistent (not rotationally invariant). Of course: it wouldn't be, because your algorithm for spin uses a fixed 180 degrees for its constant.c. As others have pointed out, you must consider Bell's Theorem. That's what I applied above. It turns out that ANY algorithm you select will run into this problem. In fact you can hand pick the outcomes - no algorithm needed - and you still cannot get the Entangled State stats when you consider 3 cases instead of 2 (again we ignore the O1 case). Yes, you were able to do it with your table. But without you realizing it, it is a "cherry picked" example. Our conclusion: no hidden variables model (which is what yours is, even though you call it public) can reproduce all of the Entangled State quantum statistics. Bell taught us this.

 

[mplummer]

Thank you for pointing out the O4 case. I understand the problem now.