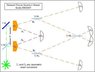
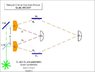
zekise said:
JesseM, thanks for the clarification. I was under the impression that you were saying D0 is a triple-hump. But now I understand you are saying that D1+D2 = D3+D4. Then please confirm for me each of the following a1 thru a6 (a1 already confirmed):
a1) D1+D2 = D3+D4 is a double hump gaussian (DHG)
Well, I agree D1+D2 = D3+D4. I don't think D3+D4 will always have a double hump--the sum of two guassians sufficiently close will only have a single hump, I believe--but whatever D3+D4 looks like in a particular setup, D1+D2 should look identical.
zekise said:
a2) Pattern D0 is invariant to the setup of delayed interferometer B (DIB), and always registers the same DHG. This is true even for delayed choice experiments.
Yes, as long as the atoms A and B emitting the photons have the same position relative to each other and relative to the screen, I believe the total pattern on the screen should always be the same, just because the alternative would seem to imply FTL or backwards-in-time signalling.
zekise said:
a3) Pattern D0 remains invariant, even if we remove DIB altogether, and idler p2 never registers.
Sure.
zekise said:
pa1) Problem with a1) - d the distance between the two slits can be arbitrarily large. Imagine d is increased to be about the size of the standard deviation of the gaussian. Then how can the anti-fringe D2 cancel out the fringe D1, so that we get a DHG and there is no hint of a fringe remaining in D1+D2. When d increases, the small "tail" of the D2 anti-fringe cannot cancel the large center body of the D1 fringe, and there will be a hint of a fringe.
How can you be sure of this, without doing any math? For example, perhaps it could be that the the further apart the distance between the emitting atoms A and B, the weaker the interference pattern, and the more D1 will resemble D3 and D2 will resemble D4.
zekise said:
Note: However, if the standard deviation of D1+D2 increases along with d, then it conceivably can be the case that the anti-fringe tail will actually cancel out the center body of the fringe. The math needs to be done to ascertain this.
Yes, I think it's necessary to do the math, but just based on principles like "no FTL signalling in QM" I feel confident that D1+D2 would always look like D3+D4.
zekise said:
a4) assume we remove D1, D2 altogether, and replace mirror Me with detector D5. I can see that we will get a fringe at D0 with half of the registrations.
Even if Me is replaced with a detector D5, that detector could still in principle measure the
momentum of incoming photons, and distinguish between ones coming from one beam-splitter vs. another; therefore the which path-information is preserved here, so I would predict no interference in this case. Even if the detector is not designed to specifically measure momentum, my guess is it would in some sense be registered by the environment (including the physical structure of the detector itself, even if it does not record this information in a form we can read); as an analogy, note that if you try to perform the double-slit experiment with electrons and you fail to create an adequate vacuum, the interaction between the electron and the air will destroy interference, even if
you don't have the technical ability to reconstruct which slit the electron went through by measuring air molecules.
zekise said:
a5) But there still remains the central paradox. Assume all 3 beamsplitters are 50%. Therefore the probability of p2 registering on D1, D2, D3, and D4 is 25% each and they are independent random variables. Now if you randomly select 25% of registration of the signal p1 on D0, you will get a double hump with 1/4 of the amplitude of D0. You will NOT get a fringe or anti-fringe.
Agreed, if you choose 25% of the signal photons at random, you will simply get a diminished version of the total pattern of signal photons.
zekise said:
The collapse of p1 will alter the wavefunction of p2. But there is no way that it can tell p2 to go to a certain detector (by defeating the beamsplitter - meaning the photon telling the beamsplitter which way it wants to go).
The collapse of each individual signal photon wavefunction can certainly alter the wavefunction of its corresponding idler in such a way as to make it more likely that particular idler will end up at a particular detector, although if you average over many randomly-selected signal photons, the average probability that a randomly-selected member of the corresponding group of idlers will end up at a particular detector should be 25%. I don't see any contradiction here.
zekise said:
If p2 is going to randomly choose D1 25% of the time, we will not get a fringe for D0|D1.
You're not distinguishing between total probability and conditional probability. if you don't include any information about the location of p1, then p2 will choose D1 25% of the time, ie P(p2 ends up at D1) = 0.25; but P(p2 ends up at D1 | p1 was detected at position x on the screen) will not necessarily be 0.25. Only when you average over all possible positions x that p1 could be detected at, weighted by the probability p1 will be detected there, do you know you'll get a probability of 0.25 [in other words, P(p2 ends up at D1 | p1 was detected at position x1 the screen)*P(p1 was detected at position x1) + P(p2 ends up at D1 | p1 was detected at position x2 the screen)*P(p1 was detected at position x2) + P(p2 ends up at D1 | p1 was detected at position x3 the screen)*P(p1 was detected at position x3) + ... = 0.25].
zekise said:
When p1 registers, neither p1 nor p2 know that this registration belongs to let's say D1. Even if they did know, there is no way to guide p2 to go and hit D1.
Well, I don't think there'd be any position on the screen where there'd be a 100% chance the idler ended up at D1--for that to happen, the D0/D2 and D0/D3 and D0/D4 patterns would have to be zero at that position while D0/D1 was nonzero, I don't think that happens anywhere. But certainly for certain positions, the probability p2 hits D2 may be higher than 25%--if you repeat the experiment many times and look only at the subset of trials where p1 hit that position on the screen, you will find that p2 is detected at D1 in more than 25% of of this subset of trials. Are you just confused about some sort of causal explanation of how this could be true, or are you disagreeing that this is what would actually be predicted by the theory of quantum mechanics?
zekise said:
You surely are not suggesting that p2 can be guided to hit a desired detector. But that is how I read this. How can you guide p2 to go through a maze of beamsplitters and hit a predetermined detector?
This question seems too classical to me, you can't just assume p2 has a single definite path while it's traveling through the apparatus, this is equivalent to assuming that every photon in the ordinary double-slit experiment must have definitely traveled through one slit or the other, even when no detector is placed at the slits. In both cases, it's better to think of a wave moving along all paths which can interfere with itself.
zekise said:
a6) Are you saying that the wavefunction for p2 is pointing to D1, ..., D4 with equal probability.
I'm not sure what it means to say the wavefunction is "pointing at" a particular detector prior to a measurement (before the photon has had time to reach any detector, the probability should be close to zero it will be detected at any of them), I would think you can only look at the amplitude squared of the wavefunction at the moment a measurement is made to find the probability the photon will be detected at different detectors at that moment. But I suppose we could say that if the measurement of the idler is made
before the measurement of the signal photon, in this case there should be an equal probability it will be detected at any of the 4 detectors (in this case it would be the wavefunction of p1 that is altered by this measurement).
zekise said:
Upon the collapse of p1, depending on where it has registered on D0, the 4 branches of p2 wavefunction coalesce onto one of the branches
I don't think that any measurement of p1 would lead to a 100% chance that p2 would be measured at a particular detector, but what I'm saying is the probabilities of p2 would be
altered by the measurement of p1, so it would not necessarily be 25% for each detector any more.
 )
)