JohnnyIngrim
- 15
- 0
I get why it's a parabola because of the x^2 (for every value of x, y is the square of that number), but why does it shift to the left (and down as well) when I add x?
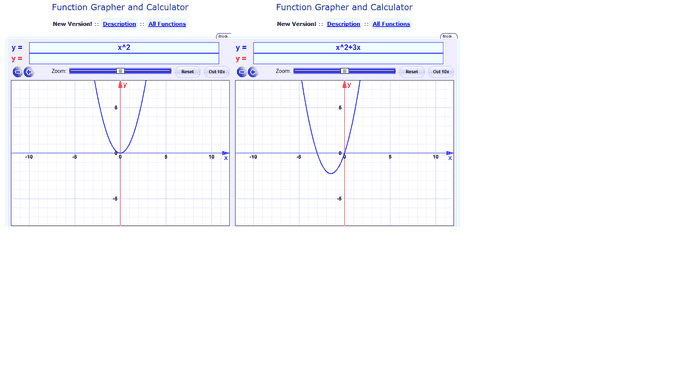
JohnnyIngrim said:I get why it's a parabola because of the x^2 (for every value of x, y is the square of that number), but why does it shift to the left (and down as well) when I add x?
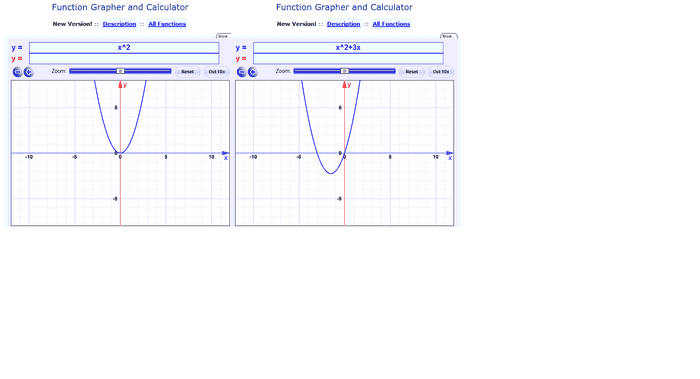
I don't get how it got to this and don't fully get what you mean.erisedk said:Try factoring x^2 + 3x. You get x(x+3). This means that the equation now has two distinct roots as opposed to the same roots. So, it intersects the x-axis at two points (0 and -3) instead of only at 0.
No, it doesn't.Dick said:x^2+3x=(x+3/2)^2-9/4. Does that form tell you why it shifts like it does? It's called 'completing the square'.
erisedk said:Try factoring x^2 + 3x. You get x(x+3). This means that the equation now has two distinct roots as opposed to the same roots. So, it intersects the x-axis at two points (0 and -3) instead of only at 0.
To find the x intercepts (roots) in the equation y = x2, you set y = 0, which means that x2 = 0. The only solution of this equation is x = 0. This means that the graph of y = x2 goes through the point (0, 0).JohnnyIngrim said:I don't get how it got to this and don't fully get what you mean.
Dick said:x^2+3x=(x+3/2)^2-9/4. Does that form tell you why it shifts like it does? It's called 'completing the square'.
The graphs of y = x2 and y = (x - a)2 have the same shape, but there vertices are in different places. The vertex (lowest point) of the first graph is at the origin (the point (0, 0)), and the vertex of the second graph is at the point (a, 0). What Dick did was use the completing the square technique to write x2 + 3x in the form (x - a)2, so he could identify the location of the vertex.JohnnyIngrim said:No, it doesn't.
So you're saying that in order to understand how the equation makes the graph I have to factor it each time? I can't look at the graph and equation and understand how the 3x causes it to shift that way, right?Mark44 said:To find the x intercepts (roots) in the equation y = x2, you set y = 0, which means that x2 = 0. The only solution of this equation is x = 0. This means that the graph of y = x2 goes through the point (0, 0).
To find the x intercepts of the equation y = x2 + 3x, you again set y = 0, and solve the equation x2 + 3x = 0. The left side can be factored to give x(x + 3) = 0, which means that x = 0 or x = -3/2. This graph crosses the x-axis at (-3/2, 0) and (0, 0).The graphs of y = x2 and y = (x - a)2 have the same shape, but there vertices are in different places. The vertex (lowest point) of the first graph is at the origin (the point (0, 0)), and the vertex of the second graph is at the point (a, 0). What Dick did was use the completing the square technique to write x2 + 3x in the form (x - a)2, so he could identify the location of the vertex.
JohnnyIngrim said:So you're saying that in order to understand how the equation makes the graph I have to factor it each time? I can't look at the graph and equation and understand how the 3x causes it to shift that way, right?
Pretty much. Different equations cause different behaviors in the graphs, though. Here are a few examples.JohnnyIngrim said:So you're saying that in order to understand how the equation makes the graph I have to factor it each time? I can't look at the graph and equation and understand how the 3x causes it to shift that way, right?
Yes and thanks. I absent-mindedly was looking at Dick's work to find the vertex. Obviously if x(x + 3) = 0, the solutions are x = 0 and x = -3. I edited my earlier post to fix what I wrote.erisedk said:Mark44, you're wrong about the graph crossing at -3/2. It's supposed to be -3.
In this particular case, you can analyze the situation graphically, but in general, you need to do as the others have advised you and factor the resulting polynomial.JohnnyIngrim said:I get why it's a parabola because of the x^2 (for every value of x, y is the square of that number), but why does it shift to the left (and down as well) when I add x?
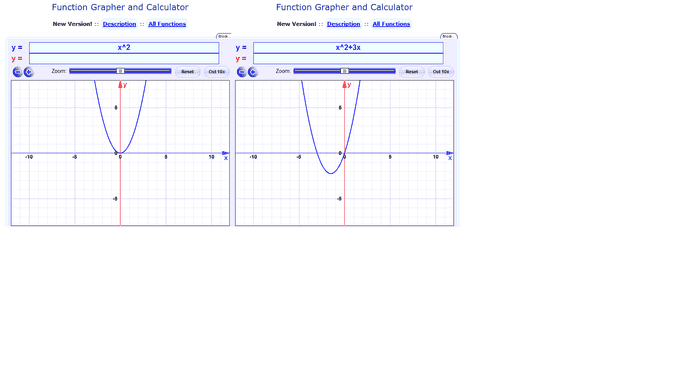
I don't get what you mean by this.vela said:If you look at the graphs of ##x^2## and ##3x##, you can see that near the origin, the ##3x## term is bigger in magnitude than the ##x^2## term