Question about Interferometer Outcomes

[ktx49]

Hey I got a quick question that I figure you guys could answer quite easily and would be easiest to understand if I just show a picture of the diagram:

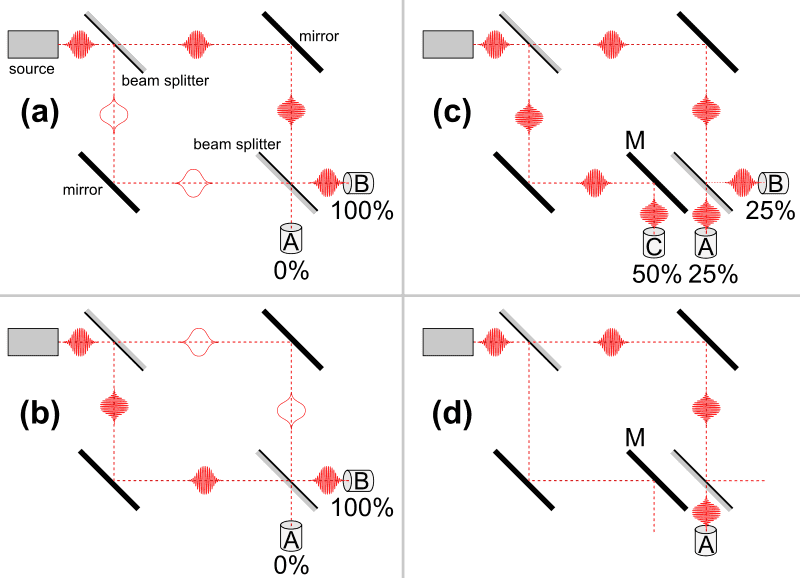
OK if we refer to figure (c) in the diagram above, how would the outcome(s) change if we replaced the mirror M with another beam splitter? (3 total beam splitters now)

thanks and sorry in advance if this is a really dumb question for some of you.

 

[mfb]

Non-polarizing beam splitters I guess?

You would get 25% below the additional beam splitter, and a partial interference at the other one. ~72.9% at B and ~2.1% at A if I did not make a mistake.

Where is the difference between (a) and (b)?

 

[ktx49]

here this is taken from the wikipedia page on Mach-Zehnder Interferometers:

Following the analysis given above, we see that in Fig. 4a and b, 100% of the output impinges upon detector B. This is true even if the light intensity is reduced so that only one photon at a time travels through the apparatus. The explanation for this is the same as for the double-slit experiment: it appears as if the wave function of each individual photon travels both paths and engages in interference at the last beam splitter, so that only the wave to B is constructive. In Fig. 4a, although the photon is illustrated as having taken the "northern" branch of the interferometer, it interferes with itself so that only detector B detects the photon. The same holds for Fig. 4b, although the photon is considered to have taken the "southern" branch of the interferometer.

Fig. 4c illustrates the situation where an obstacle has been introduced on the "southern" branch of the interferometer. 50% of the photons are deflected by mirror M, and the remaining photons are split 25% to detector A, and 25% to detector B.

Fig. 4d illustrates the fundamental paradox raised by this demonstration. An individual photon arriving at detector A must have traversed the "northern" path and could not have interacted with mirror M. The arrival of a photon at detector A constitutes proof that an obstacle exists on the "southern" path, but there is no exchange of energy between the photon and obstacle M. How could the photon possibly have acquired information about M without an exchange of energy? This is an example of counterfactual measurement in quantum physics.

and to be clear your saying the results would be ~2.1% for A, ~72.9% for B, and 25% at C?

Thanks

 

[mfb]

For your modified setup, which is not shown at Wikipedia, yes.

 

[ktx49]

thanks anyway you could quickly show me how you got the ~2.1% for A and ~72.9% for B...i can sort of intuitively understand why it would now be possible for ~2.1% of photons to reach detector A but I'd love to see the exact math for the partial interference if you get a chance.

also I'm having a hard time understanding figure (d)...why does a photon arriving at A necessarily need information about the mirror M to be possible? if the photon travels the northern path in figure (d) then it makes perfect sense it would have a 50/50 chance of making it through to A now(since its no longer possible to interfere with itself). I don't understand this:

The arrival of a photon at detector A constitutes proof that an obstacle exists on the "southern" path, but there is no exchange of energy between the photon and obstacle M. How could the photon possibly have acquired information about M without an exchange of energy?

how are those statements true? the photon doesn't necessarily need information about M to have the possibility of arriving at detector A if there is no longer a chance of interference.

the only thing paradoxical about these diagrams to me, are (a) and (b) since its obviously strange that individually fired photons can somehow create interference with themselves...however this is a well established principle of QM.

 

[mfb]

thanks anyway you could quickly show me how you got the ~2.1% for A and ~72.9% for B...i can sort of intuitively understand why it would now be possible for ~2.1% of photons to reach detector A but I'd love to see the exact math for the partial interference if you get a chance.

From the setup without M/beam splitter, we know that we get 100% constructive interference for the amplitudes at B and 100% destructive interference at A. The beam splitter reduces the intensity in that path by 50%, that reduces the amplitude by a factor of 1/sqrt(2).
Before, we had amplitudes of 1+1 at B and 1-1 at 0, now we have 1+1/sqrt(2) at B and 1-1/sqrt(2) at A. The square of those numbers is the intensity, and by comparing this to the setup without beam splitter I get the values for the intensities.

also I'm having a hard time understanding figure (d)...why does a photon arriving at A necessarily need information about the mirror M to be possible?

Without M, there is no photon detected at A. If a photon can reach A, this is an information about M.
"if there is no longer a chance of interference" is the information about M.

 

[ktx49]

I'm not saying your wrong here as your basically saying the same thing as the Wikipedia page...which seems to be the entire premise behind the "paradox" of this experiement.

However, I don't think the statement

Without M, there is no photon detected at A.

Necessarily implies the truth of the second statement

If a photon can reach A, this is an information about M.

In fact, I think we could only say that "Without M in place, there is no photon detected at A...If a photon can reach A, then M must be in place."

Intuitively I feel like what you and the wikipedia page are saying is a way of looking at this backwards...instead, it seems to me the correct way of thinking about this would be:

Without M, information is exchanged which prevents a photon from being detected at A(interference). If a photon can reach A, there is a loss of information caused by M being in place. "If there is no longer a chance of interference" is the loss of information caused by the placement of M

I'm obviously not smarter than the greatest scientific minds of the last century...I just feel like your version of things is a prime example of causality derived from counterfactual statements...so what am I missing here? what is so wrong with my version of the story per say? :)

Thanks

 

[mfb]

Well, that's the main point. The splitting process at the first beam splitter is clearly independent of the presence of M. Without M, a proper description needs "something" to travel along the lower path to get interference. With M in place, you would expect the same "something" to do that - but if you detect a photon at A, nothing is observed at M. So what did travel towards M?

 

[harrylin]

Sorry for interrupting, but is there anything non-classical about that set-up?

 

[mfb]

You can do the experiment with single photons, that is certainly non-classical.

 

[harrylin]

You can do the experiment with single photons, that is certainly non-classical.

Please explain the "certainly": I still don't see how that results in different predictions of observables (I won't hijack this thread; if it remains unclear I may start a separate thread).
Thanks.

 

[ktx49]

Well, that's the main point. The splitting process at the first beam splitter is clearly independent of the presence of M. Without M, a proper description needs "something" to travel along the lower path to get interference. With M in place, you would expect the same "something" to do that - but if you detect a photon at A, nothing is observed at M. So what did travel towards M?

i still don't get it...as far as what is traveling towards M? this is obviously the wave-function...if we put a detector at M we will certainly detect photons(look at my original question posed in this thread).

we know that a photon behaves as a wave-function until we observe it otherwise, so it makes perfect sense that if something is blocking the "waves" path that it will prevent possible interference...it doesn't require some mysterious description or paradoxical explanation...the same thing would happen if we used more classical waves.

i got to be missing something here, no?

and BTW, the experiment IS done with single photons...

 

[mfb]

this is obviously the wave-function...if we put a detector at M we will certainly detect photons(look at my original question posed in this thread).

Sure, but the wave-function always goes towards M. If you don't detect a photon at M, the wave-function magically disappears? How does it "know" that the photon got detected at A or B?
That is the non-intuitive part of quantum mechanics.

 

[ktx49]

Sure, but the wave-function always goes towards M.

correct...but it's also always going towards detectors A and B.

If you don't detect a photon at M, the wave-function magically disappears?

what do you mean detect a photon at M? its a mirror.

How does it "know" that the photon got detected at A or B?
That is the non-intuitive part of quantum mechanics.

I don't see the relevance of this? why would the photon be required to know this information to create these results? what am i missing? i don't see anything non-intuitive about this besides the normal wave/particle duality craziness of QMs...which is not paradoxical IMO, particularly in this situation. when we detect a photon it behaves as a particle, when we don't its behaving as a wave.

this seems really simple to me...the mirror M prevents the wave function from interfering with itself...hence the return of interference(partial) when we remove M and replace it with another beam splitter(the original question posed in this thread).

there need not be some mysterious exchange of information to produce these results. when the mirror M is place along the "southern path", it prevents the wave function from completing its journey along both paths which produces the interference pattern. obviously when there is no longer interference, the photons are free to reach detector A.

i can't be this dumb and I know you're not either. so what gives here?

 

[Strilanc]

I actually wrote a program to simulate this sort of thing. Here's what it shows:

The specific amplitudes of the waves are:

- 0.5+0i (25%) escapes rightward from the top
- -0.854 (~73%) escapes rightward from the bottom
- ~0.146i (~2%) escapes downward

Calculating them by hand is not too hard.

- System starts with amplitude 1 heading rightward towards top left splitter
- Splitter splits system into i/sqrt(2) reflected downward and 1/sqrt(2) continuing rightward
- The reflected downward part will gain an i factor, totaling -1/sqrt(2), after hitting the bottom-left mirror
- It will then be split into a -1/2 part escaping rightward along the bottom and a -i/2 part escaping downward
- The continuing rightward part is split into a 1/2 part escaping rightward along top and an i/2 part reflected downward towards the splitter
- The part heading towards the splitter is split into i/2/sqrt(2) escaping downwards and i*i/2/sqrt(2) escaping rightwards along the bottom

Tallying up and interfering, we have 1/2 escaping rightward along top, -i/2+i/sqrt(2)^3 ~= .146i escaping downwards, and -1/2-1/sqrt(2)^3 ~= -0.854 escaping rightward along bottom.

 

[ktx49]

^ very cool Strilanc...helps to see it visually. thanks for posting!

 

[mfb]

what do you mean detect a photon at M? its a mirror.

Okay, imagine a detector below the mirror. That does not matter, M could be a detector and the result would be the same.

I don't see the relevance of this? why would the photon be required to know this information to create these results? what am i missing? i don't see anything non-intuitive about this besides the normal wave/particle duality craziness of QMs...

It is exactly the normal wave/particle duality craziness of QM, nothing else.
It is not paraxodical, but it is unintuitive.

 

[ktx49]

i don't even see anything unintuitive about these results no matter how many times you've said it...I'm not trying to argue with you or go around in circles, so if possible could you just point out the flaw(s) in my "intuitive explanation" of these results?

even if there's a detector below the mirror like in diagram (c), we can easily understand these results in a completely intuitive manner...

the wave function always travels along both the "northern" and "southern" paths and when there is NO mirror/obstacle M along the southern path, the wave functions are free to cross paths and interfere with each other; creating the results we see in (a) and (b).

the only way its possible for a photon to be detected at A is if there's something blocking the southern path and preventing the wave functions from creating interference...i don't see how this is mysterious or requires some sort of magical exchange of information to produce these results. in fact I would wager the exact opposite, it seems that a loss of information is responsible for photon detection at A.

 

[mfb]

Using your explanation, there is no obvious reason why you always detect radiation ("a single photon") at exactly one detector, and not sometimes at two or at zero.
Sure, you can just say "this is obvious as we call it a single photon", but "photon" is just a word...

Anyway, that discussion gets pointless.

 

[Strilanc]

the only way its possible for a photon to be detected at A is if there's something blocking the southern path and preventing the wave functions from creating interference...

You're right that interferometers can generally be understood by treating the photons as classical waves. However, quantum physics treats detectors slightly differently.

If you put a detector on one path, or one detector on each, that records when photons go by, without otherwise disturbing them, QM predicts the interference will go away.

In this image, 'note time without stopping photon' detectors are represented as semi-transparent gray circles. The lack-of-interference is shown by the contributing waves being drawn overlapped instead of as a single wave (kindof hard to tell on the constructive path; the two waves just look like a darker wave):

Actually, let's step thing up a notch and make it the *noted time* that differs on the same detector, by delaying one path *before* a common detector and delaying the other path *after* (note: I'm assuming single photons at a time. If you used a stream of photons, later ones could interfere with earlier ones. I'm also assuming the detector does not maintain direction info.):

Getting rid of the detector re-introduces the interference:

and getting rid of the differing delays does as well:

The point here is that *world states* interfere, not individual photons (or so goes the many-worlds explanation). When two ways the system can split result in presents that agree on every fact of the world, you interfere those states. This naturally interferes individual photons in classical situations, while also introducing "quantum weirdness". So the photons only interfere when the detector histories are equivalent.

 

[Zafa Pi]

i don't even see anything unintuitive about these results no matter how many times you've said it...I'm not trying to argue with you or go around in circles, so if possible could you just point out the flaw(s) in my "intuitive explanation" of these results?

even if there's a detector below the mirror like in diagram (c), we can easily understand these results in a completely intuitive manner...

the wave function always travels along both the "northern" and "southern" paths and when there is NO mirror/obstacle M along the southern path, the wave functions are free to cross paths and interfere with each other; creating the results we see in (a) and (b).

the only way its possible for a photon to be detected at A is if there's something blocking the southern path and preventing the wave functions from creating interference...i don't see how this is mysterious or requires some sort of magical exchange of information to produce these results. in fact I would wager the exact opposite, it seems that a loss of information is responsible for photon detection at A.

Here is how the unintuitive argument works: "Every time I check which path the photon takes (and let it pass thru) it's possible to see results at (a) or (b). But if I'm not checking I can only see results at (b). This is crazy, the photon has to take one route or the other. Then you try to bring up something you call the "wave function", something that can't be observed. Let's call it "your fairy wave". I just want to know what the photon is doing when I'm not looking. Is it splitting in half? I never observe a half photon. And when you talk to me about your fairy wave it makes you sound like a new age buffoon. These results I observe are unintuitive!"

OK? The wave function is a mathematical devise to help you make computations, it is not something the detectors detect. When you say the mirror blocks the wave function you're mixing metaphors. The presence of the mirror causes YOU to consider a different w.f., sometimes referred to as the collapsed version, thus allowing you to make a different prediction.

 

[Zafa Pi]

- System starts with amplitude 1 heading rightward towards top left splitter
- Splitter splits system into i/sqrt(2) reflected downward and 1/sqrt(2) continuing rightward
- The reflected downward part will gain an i factor, totaling -1/sqrt(2), after hitting the bottom-left mirror
- It will then be split into a -1/2 part escaping rightward along the bottom and a -i/2 part escaping downward
- The continuing rightward part is split into a 1/2 part escaping rightward along top and an i/2 part reflected downward towards the splitter
- The part heading towards the splitter is split into i/2/sqrt(2) escaping downwards and i*i/2/sqrt(2) escaping rightwards along the bottom

Tallying up and interfering, we have 1/2 escaping rightward along top, -i/2+i/sqrt(2)^3 ~= .146i escaping downwards, and -1/2-1/sqrt(2)^3 ~= -0.854 escaping rightward along bottom.

Thank you for the clear write up. I noticed that when one part of the superposition is reflected, you multiplied it by i (like a +$\pi$/2 phase shift). Does this work for any angle of reflection (e.g. / and \ act the same way)? Is there a simple way to justify this?

 

[meBigGuy]

I'm certainly confused about the same thing as ktx49. If there is interference at the AB splitter then no particle will reach A. If there is not, then a particle can reach A. That doesn't say there is a mirror a M. It could be anywhere. It seems to just say the second path isn't there. Now the fact that a particle interferes or doesn't interfere with itself at the AB splitter by taking or not taking both paths is amazing, but I'm confused about what is being said beyond that.

 

[Zafa Pi]

Now the fact that a particle interferes or doesn't interfere with itself at the AB splitter by taking or not taking both paths is amazing, but I'm confused about what is being said beyond that.

To suggest that the particle can take both paths is a super(position)stition or interpretation. There is no such observation. The facts are: If the experimental set up is such that you can "know" what leg the photon took then there is no interference, otherwise there is interference (highly unintuitive). Any photon detected, given the lower leg is blocked, must come from the upper leg.

What is being said beyond that is the mathematics to predict that outcome and the more elaborate configurations. That mathematics is called quantum mechanics (including the superposition = the wave function). There is so much of qm that I don't know, like the question I asked Strilanc.
When Feynman said, "Nobody understands qm" I think he made a semantic error. There are many, including Feynman, who understand qm (= the mathematical theory), it's the real world (that is predicted by qm) that is unfathomable.

However, in mho the same goes for classical physics: Newton had no explanation for how a mass created its gravitational force and Einstein's refinement correlating mass with the "warping" of space-time provides no mechanism for how that is pulled off; all we have is the mathematics.

 

[meBigGuy]

To say the particle take both (all) paths is fundamental to QM. It just means that we need to sum the probabilities of all paths. The sum of path probabilities shows the interference. It is not an interpretation. Using a wave analogy is just an analogy, and leads to weirdness and confusion. The QM math is clean. If either particle becomes entangled with a measurement device, the state vectors, and the probabilities change.

When Feynman said he didn't understand QM he meant just what he said. Anyone (so to speak) can understand the math we have developed to model what we have observed.

I guess my confusion comes from me not understanding "counterfactual". I see no paradox that the sum of probabilities does not include the lower path so therefore there is no interference. I'd certainly like to understand the paradox I am missing.

 

[Strilanc]

Thank you for the clear write up. I noticed that when one part of the superposition is reflected, you multiplied it by i (like a +$\pi$/2 phase shift). Does this work for any angle of reflection (e.g. / and \ act the same way)? Is there a simple way to justify this?

I actually don't know.

In quantum computing there's phase gates that will change the phase of a single state without any other effect, so my guess is that there's optical elements that 'rotate' the photons by however much you want. The only real constraint on circuit elements is that their effect on the state vector must correspond to a unitary matrix (changing phase is, in fact, unitary).

Hypothetically speaking, placing a phase gate before or after a mirror would give you a combined element that reflects and phases by however much you want.

 

[.Scott]

Since half of the photons reaching the splitter at M will pass and the other half are reflect, I believe the result will be exactly the average between figure a and c (or figure b and c).
So
A: 12.5%
B: 62.5%
C: 25%

 

[mfb]

@.Scott: Quantum mechanics doesn't work that way. See the explanations on the previous page for details.

 

[.Scott]

@.Scott: Quantum mechanics doesn't work that way. See the explanations on the previous page for details.

I just reviewed Strilanc's post and got it.