Question about potential well schrodinger

[ChaseRLewis]

So been self-studying till this point and it has been pretty easy / generic with the PDE's. At this point though the math gets a bit more out of my depth and was curious if someone might lend a hand in helping me understand what is going on.

My question is pretty much is there a good algorithm to solve for the constants given the situation below. To solve this problem it requires an iterative method to find the constants for the wave function that meets the requirements based on the potential.

given n = 1 you get

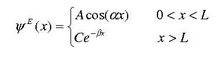
giving you the following solution for the constants alpha and beta

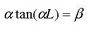
each constant having the value of

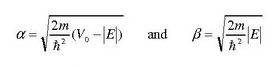
so to solve for the energy (and thus the wave equation) for an arbitrary potential value

you must solve for the constants that satisfies the potential value. (This is called an Eigenvector right?)

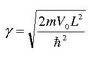
the L² is because they transformed the alpha and beta values to unitless dimensions (these are pics from a website I'm using to supplement my understanding : P easier than typing all this).

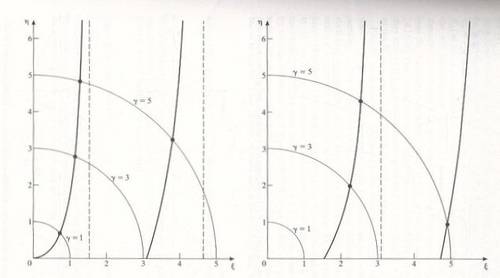TL:DR; Longwinded, question to basically ask is there a good marching algorithm to solve this type of problem for the given constants? Google isn't giving me much, at this point unfortunately.

 

[Bill_K]

A good question to ask on the Diff Eq forum.

 

[jtbell]

Put the equation in the form $\alpha \tan (\alpha L) - \beta = 0$, substitute for $\alpha$ and $\beta$, insert numerical values for all quantities except E, and use any numerical root-finding algorithm (e.g. Newton's method) to find the roots (the values of E that make the left side equal to zero).

 

[vanhees71]

It has been a long time that I've done this calculation numerically. The problem is not to find a solution but to find all solutions (energy eigenvalues). The good thing in this case is, you can easily read off from the equation, where the solutions must ly. It's easier to see by plotting the functions on the left-hand and right-hand side of the equation and look at the various branches of the tan function and the intersections of the two graphs of these functions.

Now, you know precisely boundaries between which necessarily one and only one energy eigenvalue must be located, and then the savest way is some method of nested intervals. I've been using the bisection method, which is perhaps not the fastest but a very safe way to find all the eigenvalues.

 

[ChaseRLewis]

Put the equation in the form $\alpha \tan (\alpha L) - \beta = 0$, substitute for $\alpha$ and $\beta$, insert numerical values for all quantities except E, and use any numerical root-finding algorithm (e.g. Newton's method) to find the roots (the values of E that make the left side equal to zero).

Ah root finding algorithm, I've been writing my own MATLAB code to help me visualize and do each of the equations and was trying to think of how to solve this numerically (i could easily do it in excel or a calculator just couldn't think of how to write a good algorithm that did it myself). In fact, quick doc search says MATLAB has a built-in function for finding roots. Thanks! Just couldn't find the right words.