- #1
Odal
- 29
- 1
Distance and Optical Illusions
Here is a problem which has probably a very simple solution even though it somehow eludes me.
Imagine two targets, just like those used for shooting practice or darts, on a horizontal line, but a few meters apart.
Let us say that you can hold your rifle aimed straight at the bull's eye, at a perpendicular angle relative to one target at a time, from two different positions.
You now go stand much farther away from the targets, in a straight line from your initial position. My question is, will you still have to hold your rifle at the same angle, or will you need to adjust it, making it smaller the farther you go?
If that is the case, it would mean that the objects are indeed getting smaller with the distance... Or that you only think that you are changing the angle of your aim.
Which is it?
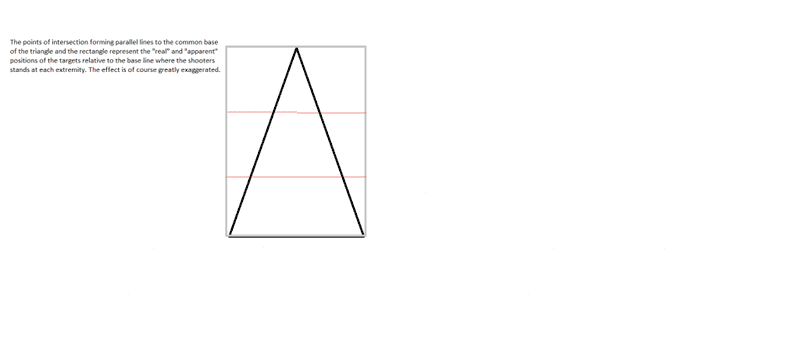
Here is a problem which has probably a very simple solution even though it somehow eludes me.
Imagine two targets, just like those used for shooting practice or darts, on a horizontal line, but a few meters apart.
Let us say that you can hold your rifle aimed straight at the bull's eye, at a perpendicular angle relative to one target at a time, from two different positions.
You now go stand much farther away from the targets, in a straight line from your initial position. My question is, will you still have to hold your rifle at the same angle, or will you need to adjust it, making it smaller the farther you go?
If that is the case, it would mean that the objects are indeed getting smaller with the distance... Or that you only think that you are changing the angle of your aim.
Which is it?