- #1
TheCelt
- 24
- 5
Hello
I am trying to teach myself some basic maths for astronomy from a book, namely trying to calculate the distance between two stars in a binary system.
One thing i am confused with is what angular separation means and how it can be translated to true physical distance between them using trigonometry. I am trying to visualise it but its a bit confusing at the moment. The book did not explain it as it seems to have presumed i already understood this.
Firstly what does it mean for each star to have an angular separation from centre of mass, eg if star A has 5 arcsec and star B has 10 arcsec what are these angles relative to? And if you know the distance D of the system from Earth, i presume trigonometry can be done to solve it but i am struggling to visualise how to draw it out to do the trigonometry for it at the moment.
I made a drawing to show the setup of what i think it might mean:
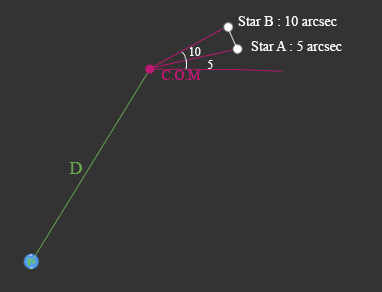
When they say angular separation from COM is this correct thinking? If so how are they defining the angle? What constitutes the 0 arcsec line, what counts as the positive x-axis in space i guess is what I am asking.
Secondly from that i do not understand how you might calculate the physical separation distance between the two stars (white line magnitude). Mainly because i am confused by the angle situation.
I am trying to teach myself some basic maths for astronomy from a book, namely trying to calculate the distance between two stars in a binary system.
One thing i am confused with is what angular separation means and how it can be translated to true physical distance between them using trigonometry. I am trying to visualise it but its a bit confusing at the moment. The book did not explain it as it seems to have presumed i already understood this.
Firstly what does it mean for each star to have an angular separation from centre of mass, eg if star A has 5 arcsec and star B has 10 arcsec what are these angles relative to? And if you know the distance D of the system from Earth, i presume trigonometry can be done to solve it but i am struggling to visualise how to draw it out to do the trigonometry for it at the moment.
I made a drawing to show the setup of what i think it might mean:
When they say angular separation from COM is this correct thinking? If so how are they defining the angle? What constitutes the 0 arcsec line, what counts as the positive x-axis in space i guess is what I am asking.
Secondly from that i do not understand how you might calculate the physical separation distance between the two stars (white line magnitude). Mainly because i am confused by the angle situation.