Question involving some reasoning.

  • Thread starter Thread starter azatkgz
  • Start date Start date
Click For Summary
SUMMARY

The problem involves fifty gangsters positioned on a plane, each shooting at the closest gangster simultaneously. The conclusion drawn from the discussion is that the minimal number of dead bodies is ten, achieved by grouping the gangsters into five circles where only the two central gangsters in each circle are killed. This solution is based on the assumption that gangsters shoot the closest target, leading to a strategic arrangement that minimizes casualties.

PREREQUISITES
  • Understanding of geometric arrangements and spatial reasoning.
  • Familiarity with basic principles of game theory.
  • Knowledge of simultaneous actions in mathematical modeling.
  • Ability to visualize and analyze two-dimensional configurations.
NEXT STEPS
  • Explore geometric configurations in game theory.
  • Research mathematical proofs related to simultaneous actions.
  • Study optimization strategies in competitive scenarios.
  • Learn about spatial reasoning techniques in mathematics.
USEFUL FOR

Mathematicians, game theorists, and anyone interested in strategic decision-making in competitive environments.

azatkgz
Messages
182
Reaction score
0

Homework Statement


Fifty gangsters on a field are shooting each other simulteneously.Assume that
i.Gangsters are points on the plane.
ii.Gangsters don't miss,so once he shoots at someone,the target is killed.
iii.Each gangster shoots the one that is closest to him(or any of the closest ones if they are on same distance from him)

What is the minimal number of dead bodies?They shoot each other just once,all fifty at the same moment.Guess the answer and then try to prove it.





The Attempt at a Solution


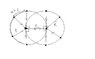
I divided 50 gansters to 5 groups.In each group only 2 gansters in the center of circle are dying(see picture).With arrows I showed direction of shooting.So my answer is only 10 gansters.
 

Attachments

  • Gansters.jpg
    Gansters.jpg
    14.5 KB · Views: 459
Physics news on Phys.org
I'm no mathematician but it looks good to me.
 

Similar threads

Wall thickness of ring habitats for radiation shielding
  • · Replies 4 ·
Replies
4
Views
4K
Decompose 4x4 determinant into 24 determinants -- How many are zero?
  • · Replies 1 ·
Replies
1
Views
2K
High School Question about quantum superposition
  • · Replies 2 ·
Replies
2
Views
3K
High School Questions about momentum and force as well as normal force/friction
  • · Replies 35 ·
2
Replies
35
Views
5K
Graduate Charged particles through various B field shapes quesion
  • · Replies 3 ·
Replies
3
Views
2K
Make 2 launchers that shoot a straw with clay at the end
  • · Replies 3 ·
Replies
3
Views
2K
High School Help with understanding the Doppler effect
  • · Replies 64 ·
3
Replies
64
Views
8K
Graduate Arrows vs. Plate Armor: Kinetic Energy & Momentum Test Results
  • · Replies 7 ·
Replies
7
Views
6K
Undergrad Hidden phase in polarization tests of Bell's inequality?
  • · Replies 49 ·
2
Replies
49
Views
6K
Who Wins the Three-Way Duel in The Good, The Bad, and The Ugly?
  • · Replies 1 ·
Replies
1
Views
3K