Question on problem 2.16 (a) of the Feynman Lectures (two-mass pulley)

[tomul]

Homework Statement

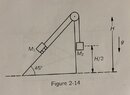
There is a mass-pulley system as shown in the attachment. I am asked to find the acceleration of M2 with M2 > M1.

Relevant Equations

acceleration of free fall : g
sinθ = O / H

My attempt was to calculate the acceleration of M2 as the acceleration of M2 if it were the only mass in the system, minus the component of M1's acceleration along the slope. And then I would divide the whole thing by 2 to get the acceleration for just one of the two masses@

a = 1/2 ( g - [acceleration of M1 along slope] )

Based on what I've seen online, this approach seems to be correct, however I think I'm resolving the acceleration incorrectly. The angle in the triangle is 45 degrees, so taking the sine of this will give sin 45 = O / H. The opposite should be the acceleration downwards due to gravity and since weight acts downwards, I figured this should just be free fall acceleration, g. So to get the component along the slope I would need to rearrange for H. sin45 = g / H becomes g / sin45 = H. So:

a = 1/2 (g - g/sin45)
a = g/2 (1-1/sin45)

But it seems the actual answer is:

a = g/2 (1 - sin45)

I can only think that I must have resolved the acceleration incorrectly...

 

[Orodruin]

When you make a projection of a force into components, you need to draw a line orthogonal to the direction you project on, not orthogonal to the force.

 

[Steve4Physics]

Hi @tomul. Welcome to PF. Your approach seems based on 'hunches' (and is wrong)!

One good way to partially check an answer is to consider an extreme case. Suppose M₂ is very large compared to M₁. You could even consider M₁=0. What would you expect to happen?

I hope you can see that M₂'s acceleration should be very nearly equal to g.

This is not consistent with either your answer or the 'official' answer. So something is wrong.

The correct answer is a formula which includes both M₁ and M₂.

I suggest you:
- check you have got the question and 'official' answer correct;
- read (or watch videos) about how to solve simple Atwood Machine problems';
- find out how to resolve a force into componente. I once made a video about this starting from basics. If you think it would help, here it is: