Buzz Bloom
Gold Member
- 2,517
- 465
The diagram below is from https://en.wikipedia.org/wiki/Galaxy_rotation_curve .
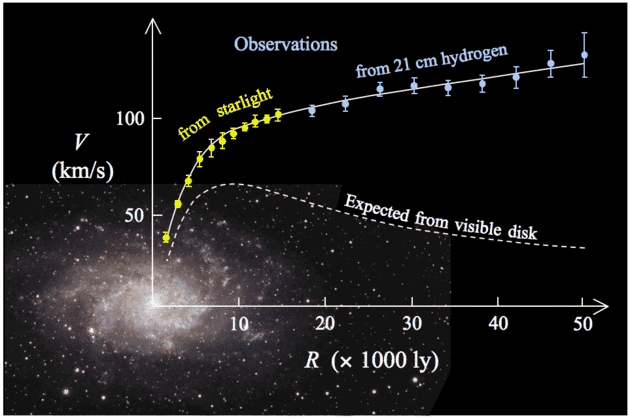
I would much appreciate a derivation explaining the shape of the "Expected from visible disk" curve in the diagram. Naively, based on Newtonian mechanics for the orbital velocity of a circular orbit,
I would much appreciate a derivation explaining the shape of the "Expected from visible disk" curve in the diagram. Naively, based on Newtonian mechanics for the orbital velocity of a circular orbit,
V = √GM/R ∝ 1/R1/2 .
Obviously, this is not the shape of the diagram curve. I suppose the diagram curve towards the right might be close to the above formula, but what is the derivation for the shape of the left part of the curve?