- #1
Mohdoo
- 20
- 0
Hello! I have been working on this problem for around 1.5 hours, and decided I simply need help.
"Using branch-current analysis, find the magnitude and direction of the current through each resistor for the network.
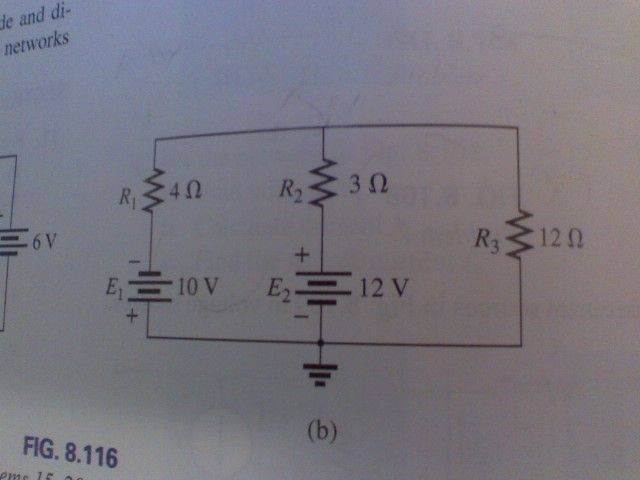
I tried using kirchhoffs current law? :D
I tried using various attempts at the loop, first trying using the 10V voltage source as positive, then minus, then same with the 12v, but I just can't seem to get it quite right.
When I eventually did (-10 -4I1(3.06) +3I2(3.25)+12), I got -.4900. Am I perhaps supposed to convert these Voltage sources to current sources? I am totally lost here.
Thanks!
Homework Statement
"Using branch-current analysis, find the magnitude and direction of the current through each resistor for the network.
Homework Equations
I tried using kirchhoffs current law? :D
The Attempt at a Solution
I tried using various attempts at the loop, first trying using the 10V voltage source as positive, then minus, then same with the 12v, but I just can't seem to get it quite right.
When I eventually did (-10 -4I1(3.06) +3I2(3.25)+12), I got -.4900. Am I perhaps supposed to convert these Voltage sources to current sources? I am totally lost here.
Thanks!