B Questions about a normal distribution (discrete to continuous)

[PainterGuy]

TL;DR Summary

I was trying to understand normal distribution and had a couple of questions.

Hi,

I was watching this Youtube video (please remove the parentheses) :
https://youtu.(be/mtH1fmUVkfE?t=215)

While watching it, a question came to my mind. In the picture, you can easily calculate the total number of customers. It's 1000.

For my question, I'm going to use the same picture. I hope you get the point.

What if the data was continuous something as shown below. How do you calculate the total number of customers? Wouldn't the number be infinite because between any two numbers, e.g. between '2' and '3', there is an infinite set of values? I'm not sure if the question really makes sense.

Could you please guide me?

In case of normal distribution the curve also represents continuous data but I believe, practically, it's discrete data made up of very thin slices as shown below and later curve fitting is used to get a continuous curve.

Thank you!

 

[BvU]

What if the data was continuous

That's a bit difficult with 'number of ice creams'
Think of an intermediate step: at the grocery store: money spent per customer. With a sample of 1000 customers there will likely be 1000 customers in the bin 0 - 1000 $
But for the bin 0-100 $ the first bin will be close to 1000 and the second the remainder (more or less).
Binning from 0-10, 10-20 etc will give a wider distribution with less customers per bin. Still the total number will be 1000 if you add all the bins.
etc.

It's a matter of dimension: number per bin width times bin width = number. If the bin width is taken smaller, bins will contain proportionally less, but the sum of all bin contents will remain the same.

For a continuous distribution the vertical dimension is usually the probability density : the probability is found by multiplying with the horizontal 'bin width'.[edit] by the way, your question applies to all distributions, not just normal distributions.

 

[Stephen Tashi]

In case of normal distribution the curve also represents continuous data but I believe, practically, it's discrete data made up of very thin slices as shown below and later curve fitting is used to get a continuous curve.

No. You are confusing the concept of a probability distribution with the concept of a histogram of data. A continuous probability distribution is a mathematical formula, not a histogram of data. A probability distribution gives information about the probable values of one sample of a random variable. If you take 100 independent samples of the same random variable and histogram the results then the histogram can have various shapes. The distribution of the random variable does not determine a unique shape for the histogram of the data. The probability distribution can be used to calculate the probability that the histogram of data has various shapes.

 

[PainterGuy]

Thanks a lot!

Think of an intermediate step: at the grocery store: money spent per customer. With a sample of 1000 customers there will likely be 1000 customers in the bin 0 - 1000 $
But for the bin 0-100 $ the first bin will be close to 1000 and the second the remainder (more or less).

In my humble opinion, it would depend upon the customers. Generally, as you are suggesting, most customers don't spend more than $100 in a grocery store. But It's possible that the second bin $100-200 could capture a big chunk of 1000 customers compared to $0-100 bin, at least on certain days. I just wanted to point this out.

If you take 100 independent samples of the same random variable and histogram the results then the histogram can have various shapes. The distribution of the random variable does not determine a unique shape for the histogram of the data. The probability distribution can be used to calculate the probability that the histogram of data has various shapes.

How can the probability distribution be used to calculate the probability that the histogram of data has various shapes? The distribution gives the most probable numeric guess about something. Yes, if one knows the probability, p, of something might happen, one can also calculate of probability, 1-p, that it might not happen.

I think that the problem could be stated as follows. We know the probability that something will happen. If a trial or experiment is done, say, 30 times, how its probability will vary in each experiment. Should Binomial formula be used?

Thank you!Note to self:
Check Statistics by Levin, Rubin 7th ed, graphing frequency distribution, page 38-41 kindle version

Helpful link(s):
1: https://www.statisticshowto.datasciencecentral.com/choose-bin-sizes-statistics/
2: https://www.quora.com/What-is-the-difference-between-probability-and-probability-distribution
3: https://help.plot.ly/histogram/

 

[BvU]

Note that what is usually given and plotted is a probability density function $P$.
With the property (for a single stochastic variable)$$\int_{-\infty}^{+\infty}P(x)\,dx = 1 $$and one can calculate the probability to find $x$ between $x_1$ and $x_2$ from $$\int_{x_1}^{x_2}P(x)\,dx$$

e.g. in the normal distribution lemma they clearly say $f$ is a density

How can the probability distribution be used to calculate the probability that the histogram of data has various shapes?

It can't (the question is a bit vague, too)

The probability density function (pdf) can be used to calculate the probability that an observed value falls in a given bin.
Example: between $\mu+\sigma$ and $\mu + 2 \sigma$ the probability is 0.1359 for the $f$ in the link.

How many of $N$ ($N$ big) observations end up in a bin for which the pdf gives a probability $p$ is again a stochastic variable that is Poisson distributed with mean $pN$.
I.e. if you repeat your set of $N$ observations a (big) number of times and then make a histogram of the number of observations in this particular $p$ bin per set, you should get a Poisson distribution with mean $pN$.

Phew...

 

[Stephen Tashi]

I think that the problem could be stated as follows. We know the probability that something will happen. If a trial or experiment is done, say, 30 times, how its probability will vary in each experiment. Should Binomial formula be used?

If we know the probability that something will happen then it's probability does not vary. I think you are confusing the concepts of frequency (how often something actually happens in a series of experiments) with the concept of probability.

As mentioned before, there can be no guarantee that an event with probability $p$ will happen with a frequency of $p$. Such a definite connection would contradict the concept of probability. Likewise if an event happened with a frequency of f in 100 independent trials then there is no mathematical law that says the probability of it happening in one trial is f.

The distribution gives the most probable numeric guess about something.

In general, that's not correct. I think what you mean is that if an event happens M times in N independent trials then M/N is, in an inuitive sense, the "best" guess for the probability of the event happening in a single trial. The mathematical justification for guessing M/N is that assuming the probability of the event is p= M/N is the numerical value that makes the observed frequency M/N the most probable outcome. This says nothing about the probability that p =M/N. Without an assumed probability distribution for various values of p, you can't say anything about the probability that p = M/N.

To illustrate a scenario where the value of p can have an associated probabiliy, consider the following scenario:
A box contains 3 coins. One coin has probability p = 1/2 of landing heads, the other two coins have probability p = 2/3 of landing heads. A coin is picked at random from the box and filipped 5 times. It lands heads 3 of those times. What is the probability that p for the selected coin is 3/5? The probability that p = 3/5 is zero because we know that the only possible values of p are 1/2 and 2/3.Guessing M/N is a specific example of the procedure of using "maximum likihood estimation". Like many statistical techniques, maximum liklihood estimation is a procedure, not an axiom or law that is absolutely guaranteed to produce the "best" result for all specific ways to define "best".

How can the probability distribution be used to calculate the probability that the histogram of data has various shapes?

First you must define the shape you are interested in. Then pose the problem as a specific question about probability. For example, suppose the distribution is a normal distributiion with mean 0 and variance 1. Suppose the histogram of interest had 4 bins defined by [-2,-1], [-1,0], [0,1],[0,2] and represents the result of 5 independent realizations of the random variable with results : 1 outcome in bin [-2,-1], two outcomes in bin [-1,0], two outcomes in bin [0,1]. Calculating the probability of such a histogram is a specific problem in probability. The calculation would involve "binomial coefficients", but not the "binomial distribution".

As @BvU indicates, for similar problems involving a large number of bins and a large number of outcomes, it gets too complicated to compute the numerical answer.

 

[PainterGuy]

Thank you very much!

I would like to expand on the previous two replies but first I need to clarify something.

Suppose an event is capable of being repeated sufficiently large number of times “N”, and the frequency of the desired outcome is “f ”. Then relative frequency of the outcome is “ f ⁄ N”. The limiting value of the relative frequency can be used to define probability of the outcome.
[Levin, Richard I.. Statistics for Management (p. 160). Kindle Edition. ]

To illustrate several of these distributions, consider a situation at Kerr Pharmacy, where employees are often late. Five workers are in the pharmacy. The owner has studied the situation over a period of time and has determined that there is a 0.4 chance of anyone employee being late and that they arrive independently of one another.
[Levin, Richard I.. Statistics for Management (p. 227). Kindle Edition.]

How would the owner determine the probability of 0.4? Suppose on day #1, one employee is late, i.e. 1/6, on day #2 two employees are late, i.e. 2/6, and so on. The owner could carry on this observation for 60 days, i.e. N=60.

Would the owner proceed as follows to calculate the probability of 0.4?

Note to self:

Note that what is usually given and plotted is a probability density function $P$.
With the property (for a single stochastic variable)$$\int_{-\infty}^{+\infty}P(x)\,dx = 1 $$and one can calculate the probability to find $x$ between $x_1$ and $x_2$ from $$\int_{x_1}^{x_2}P(x)\,dx$$

e.g. in the normal distribution lemma they clearly say $f$ is a density

P(x) is probability density function where probability density, PD=probability/bin_width. Please refer to 3rd link under "Helpful link(s)" and also check page #232 of Levin, Ruben book, 7th ed, Kindle, to see how binomial could change into normal distribution as n becomes infinite. So, when you are integrating, you are summing up infinitesimal sections, {probability/dx}*dx where "x" could be molecules speeds or anything else. The main thing is that the result of integration is a scalar without any units; it gives total probability between two values of 'x'.

It can't (the question is a bit vague, too)

The probability density function (pdf) can be used to calculate the probability that an observed value falls in a given bin.
Example: between $\mu+\sigma$ and $\mu + 2 \sigma$ the probability is 0.1359 for the $f$ in the link.

Have a look here.

Helpful link(s):
1: https://www.britannica.com/topic/Poisson-distribution
2: https://stattrek.com/probability-distributions/poisson.aspx

 

[Stephen Tashi]

I would like to expand on the previous two replies but first I need to clarify something.

Suppose an event is capable of being repeated sufficiently large number of times “N”, and the frequency of the desired outcome is “f ”. Then relative frequency of the outcome is “ f ⁄ N”. The limiting value of the relative frequency can be used to define probability of the outcome.
[Levin, Richard I.. Statistics for Management (p. 160). Kindle Edition. ]

That is not the mathematical definition of probability. You can find books on statistics that give intuitive definitions for concepts used in statistics. Intuitive definitions are useful for thinking intuitively, but taking them seriously and literally is a handicap in doing mathematics.

A definition based on the concept of a llimiting fequency doesn't tell us how to analyze data from a finite number of experiments. The intuitive definition you quoted is using the phrase "an event is capable of being repeated sufficiently large number of times “N”, to deal with the mathematical concepts of independent and identically distributed random variables. However, to define the mathematical concept of "independent" events requires making statements about their probabilities, so trying to define the probability of an event by using the concept of independent events would produce a circular definition.

How would the owner determine the probability of 0.4?

Would the owner proceed as follows to calculate the probability of 0.4?

The passage you quoted simply assumes p = 0.4, so I think you are considering a problem that is beyond the scope of that section of your text.

If you are asking the above questions in the sense of "What is the unique answer based on the given data?" you don't yet understand the conceptual framework for statistical estimation. Perhaps your text deals with statistical estimation in later chapters.

A person who uses a phrase like "how do we calculate..." suggests that the given information plus logic and mathematics is sufficient to deduce a specific answer. A person who uses the phrase "how can we estimate..." leaves open the possibility that some additional assumptions must be made in order to get a definite result.

The two major categories of statistical methods are 1) Estimation and 2) Hypothesis Testing. A set of data, by itself, does not tell us how to estimate the parameters of a probability distribution. Various procedures of statistical estimation make different assumptions, set different objectives, and can get different answers. It is the nature of probabilistic phenomena, that no method of estimation will always produce the true value of a parameter. A result from a statistical method is only "correct' in the sense that it is the correct answer to a problem that is stated using the data plus additional assumptions and objectives.

One method of statistical estimation is Moment Matching. In the example, there are (5)(60) = 300 opportunities for an absence. In those opportunities there occurred a total of:
(1)(24)+2(20)+3(11)+4(3)+5(2)=119 absences. Model the distribution as a binomial with N = 300 and probability of success $p$. The mean of the distribution is $Np = 300p$. Set our objective as matching the observed number of absences in the data equal to the mean number of absences for the distribution. This defines the problem as solving $300p = 119$ for $p$.

Instead of matching the mean (first moment) of a binomial distribution to the mean of the data, one could take the approach of matching the variance of the data to the variance of the distribution.

Which method would be best? That depends on the conceptually complicated ways of defining "best"!

 

[PainterGuy]

Thank you!

That is not the mathematical definition of probability. You can find books on statistics that give intuitive definitions for concepts used in statistics. Intuitive definitions are useful for thinking intuitively, but taking them seriously and literally is a handicap in doing mathematics.

I understand your point. But, in my humble opinion, when someone starts learning a concept or subject, it's okay to start with simple, a little bit informal, and intuitive definitions which are not very rigorous and precise. At the same time, one should always bear in mind that as the conceptual progress is made, one needs to evolve the defining framework, and work out and accept more rigorous framework of the subject. Actually, academically, this is what is done in every subject and it seems to work. For example, a simple framework of atomic models and atomic particles are later refined and formalized using quantum theory models, concepts of numbers such as natural, real, complex are gradually formalized, concepts of limit which is later rigorously defined using delta epsilon definition, etc. Pedagogically, refining a concept in small steps is a best to learn something, in my view. I believe that you are saying the same thing.

One method of statistical estimation is Moment Matching. In the example, there are (5)(60) = 300 opportunities for an absence. In those opportunities there occurred a total of:
(1)(24)+2(20)+3(11)+4(3)+5(2)=119 absences. Model the distribution as a binomial with N = 300 and probability of success p.

Well, how do I graph such a binomial distribution with N=(5)(60)=300 where "5" is number of employees, "60" is number of observed days. Initially, I assumed that N=60 and I could picture it where x-axis represented number of late arrivals from '0' to '5', and y-axis represented probability of those late arrivals. In case of "300", I think it represents each opportunity of being late but how do I relate the probability of an employee being late to it? For the proper context I'm quoting some sections on the same example from the same book. In Picture #2, the author also uses n=10 and n=30 cases to show that how the binomial starts looking like normal distribution once the sample size, i.e. number of employees, increases. Thank you!

Picture #1: https://imagizer.imageshack.com/img921/7509/xJaZOg.jpg
Picture #2: https://imagizer.imageshack.com/img921/1979/64jLcB.jpg
Note to self:

How many of $N$ ($N$ big) observations end up in a bin for which the pdf gives a probability $p$ is again a stochastic variable that is Poisson distributed with mean $pN$.
I.e. if you repeat your set of $N$ observations a (big) number of times and then make a histogram of the number of observations in this particular $p$ bin per set, you should get a Poisson distribution with mean $pN$.

To apply Poisson distribution, average or mean, is required, and to calculate it you need to know the probability, mean = λ = np, where n is number of trials and p is probability.

Check this link: https://www.britannica.com/topic/Poisson-distribution and check Levin, Richard I.. Statistics for Management (p. 239). Kindle Edition. Check post #7 and #8 to get an idea how to calculate probability.

The Poisson distribution will tell you the probability of each observation ending up into a bin with probability p.

 

[Stephen Tashi]

Pedagogically, refining a concept in small steps is a best to learn something, in my view. I believe that you are saying the same thing.

In a college level statistics course, I think it's best to follow the standard mathematical presentation of probability theory. This includes the concept of a probability space, which is a probability measure, a set of outcomes, and an algebra of subsets of outcomes. Without much harm those concepts can be presented as the special cases of "a sample space for an experiment" consisting of a "probability distribution" over a "range of values", and limiting the subsets considered to sets consisting of intervals and single points.

Presenting the concept of probability as a limiting frequency is something I'd expect in course designed for people who only need to do statistical calculations by rote - perhaps lab technicians, inspectors in factories - maybe managers!

You are asking questions that go beyond the material in your textbook, so I assume you want to deal with statistics at a college level.

Well, how do I graph such a binomial distribution with N=(5)(60)=300 where "5" is number of employees, "60" is number of observed days.

The binomial distribution I used has the parameters N = 300 and p. So it doesn't have any parameter representing the 5. If we take seriously the idea that each lateness by each employee is an independent event, the fact that data is collected in groups of 5 doesn't matter. It's like flipping a coin 300 times and recording the data. Grouping the data in sets of 5 records doesn't add anything to the information it contains.

I agree that using a binomial distribution with N=300 does not model the fact that at most 5 employees can be late on a given day. However, if you grouped the coin flip data in sets of 5, that would automatically impose such a constraint.

To repeat an earlier point, a histogram of data (or a table of data) and a probability distribution are different things. So if you pick a probability distribution for the data, you don't necessarily get a probability distribution whose graph involves all the parameters involved in a table or histogram of the data.

Initially, I assumed that N=60 and I could picture it where x-axis represented number of late arrivals from '0' to '5'

That's reasonable way to represent a binomial distribution where N = 5. The 60 days of data are not represented on the graph and they don't need to be. A distribution for a random variable gives the probabilities for the outcomes of a single realization of a random variable.

Students taking introductory statistics are tempted to think that a statistics problem will involve exactly one random variable and its distribution. Perhaps that will be true in Chapter 1, but even moderately sophisticated problems involve several different random variables. In the example at hand, we can consider the random variable that answers the question "How many employees are late today"? We can consider a different random variable that answers the question "How many latenesses are there in 300 opportunities for a lateness to occur?".

In the example at hand, we might choose to model the number of employee latenesses on a given day by some non-binomial distribution. For example, we might think the latenesses are not independent events. Perhaps some employees depend on others for a ride to work. Let the random variable $X$ answer the question "How many employees are late today?". Suppose we consider what happens each day to represent an independent realization of $X$ (i.e. we ignore things like hangovers on Monday mornings)
We can define another random variable $Y$ that answers the question "How many latenesses occur in 60 days?". If we have specific distribution for $X$ we can compute the distribution for $Y$ by the procedure of "convolution".

Probability distributions can be defined on outcomes in two-dimensional spaces. If we want to consider things like hangovers on Mondays, we can pick a model where the distribution is a function of two variables $f(k,d)$ where $k$ is the number of employees absent and $d$ is the day of the week: 1,2,..7.

 

[PainterGuy]

Thank you very much!

You can find the full example of employees here (ignore the highlights): https://imagizer.imageshack.com/img922/6692/uuUrm0.jpg

The binomial distribution I used has the parameters N = 300 and p. So it doesn't have any parameter representing the 5. If we take seriously the idea that each lateness by each employee is an independent event, the fact that data is collected in groups of 5 doesn't matter. It's like flipping a coin 300 times and recording the data. Grouping the data in sets of 5 records doesn't add anything to the information it contains.

I agree that using a binomial distribution with N=300 does not model the fact that at most 5 employees can be late on a given day. However, if you grouped the coin flip data in sets of 5, that would automatically impose such a constraint.

I will focus on the case of n=10 from the lateness example, plot is shown below.

Initially it was said that n=5 is total number of employees and r is number of late arrivals. If n=10 and r=10, how do these relate to the original number of employees and late arrivals? Let's try to find an answer.

Originally, the maximum possible number of late arrivals was 5, as is shown below. Assume that the data set was collected over a period of two weeks. Suppose that the owner collects another independent data set over the period of two more weeks. Now there are two independent data sets conveying the same information.

We notice that for n=5, the probability for two late arrivals, i.e. r=2, is 0.3456. But when n=10, the probability for r=4 is 0.2508; 0.3456 - 0.2508 = 0.0948. What does this difference tell us? I'd say that it mean that the probability of two employees being late in both of the data sets, i.e. r=2+2, is 0.2508.

We can see below that when n=30, which according to my understanding means 6 independent data sets, the probability for r=2+2+2+2+2+2=12 is 0.14738.

Do I make any sense at all?

Thanks a lot your time and help!

 

[Stephen Tashi]

Originally, the maximum possible number of late arrivals was 5, as is shown below. Assume that the data set was collected over a period of two weeks. Suppose that the owner collects another independent data set over the period of two more weeks. Now there are two independent data sets conveying the same information.

I'd say that it mean that the probability of two employees being late in both of the data sets, i.e. r=2+2, is 0.2508.

If $q$ is the probability of something happening in one experiment, then $q^2$ is the probability of it happening in each of two given independent experiments. Check your idea against that fact.

 

[PainterGuy]

Thank you!

For n=5, the probability for two late arrivals, i.e. r=2, is 0.3456, and when n=10, the probability for r=4 is 0.2508.

0.3456² = 0.1194 ≠ 0.2508

I'm wrong so I'm back to the original question as quoted below. Could you please guide me with this?

We notice that for n=5, the probability for two late arrivals, i.e. r=2, is 0.3456. But when n=10, the probability for r=4 is 0.2508; 0.3456 - 0.2508 = 0.0948. What does this difference tell us?

 

[Stephen Tashi]

Think precisely about the outcomes in "sample spaces" involved. A detailed way to define the outcomes of an experiment that can answer "How many employees are late today" in the case of 5 total employees is to use probability space $\Omega_a$ , each of whose outcomes is a sequences of 5 zeroes or ones. For example:

(1,1,1,1,1), (0,1,1,1,1), (1,0,1,1,1), ... (0,0,0,0,0) where a "0" in the 3rd place indicates employee 3 is late, etc.

For outcomes in the case of 10 total employees, we can use probability space $\Omega_b$ whose outcomes are sequences of 10 zeroes and ones like:
(1,1,1,1,1,1,1,1,1,1) or (0,1,1,1,1,1,1,1,1,1), etc.

For the experiment to answer "How many employees are late on day 1 and how many employees are late on day 2", the we can use probability space $\Omega_c$, whose outcomes are a pair of sequences like:

( (1,1,0,0,1),(0,1,1,0,0)) or ((1,1,0,0,1),(1,1,1,1,1)) etc.

The set "two employees are late on both days" in $\Omega_c$ does not contain all pairs of sequences with 4 total latenesses For example it does not include ( (0,0,0,1,1)(1,1,1,0,1) ).

However, in the sample space $\Omega_b$ we do include sequences like (0,0,0,1,1,1,1,0,1). So the set of outcomes defined by "4 employees are late out of 10 total employees" in $\Omega_b$ is a larger set than the set defined by "On both days, 2 out of 5 employees are late" in $\Omega_c$.

$\Omega_b$ and $\Omega_c$ have the same total number of outcomes and we are assuming each outcome is equiprobable. So comparing the probability of sets between them only involves counting the elements in the sets.Edit: Instead of say that each outcome is "equiprobable", I should say that each outcome on one sample space has a corresponding outcome in the other sample space that has the same probability.

 

[PainterGuy]

Thank you!

I'm sorry that I'm going to ask about the same problem again. But I believe that you are approaching the problem differently.

In post #11 above, this example, https://imagizer.imageshack.com/img922/6692/uuUrm0.jpg, was discussed. I was mainly focused on the plots at the bottom where n=10 and n=30.

The following was my interpretation for n=10 case. As there were 5 employees, n=5, therefore the maximum possible number of late arrivals was also 5, i.e. r=5. Assume that the data set was collected over a period of two weeks. Suppose that the owner collects another independent data set over the period of two more weeks. Now there are two independent data sets conveying the same information. The combined elements of both data sets are 10. I was assuming that the actual number of employees does not change and I was trying to interpret what n=10 actually means.

Well, it looks like that my underlying interpretation is wrong. When, n=10, it might mean that the actual number of employees is really 10 instead of 5. Perhaps, the author was trying to show that how probabilities are affected when number of employees change from 5 to 10 and 30.

Thanks a lot!

 

[Stephen Tashi]

I'm sorry that I'm going to ask about the same problem again. But I believe that you are approaching the problem differently.

How would you define "the problem"? I haven't seen a specific problem stated.

Perhaps, the author was trying to show that how probabilities are affected when number of employees change from 5 to 10 and 30.

It looks like the author is trying to illustrate the idea that a binomial distribution B(n,p) for large N can be approximated by a normal distribution. What precisely does "can be approximated" mean? How would you, or the textbook author do the approximation?

 

[PainterGuy]

Thank you!

How would you define "the problem"? I haven't seen a specific problem stated.

Actually, I was trying to understand it for myself that if the assumption of 5 employees could hold even when n=10, or n=30?

If you watch this video until 4:33, it shows how the distribution starts looks like a bell curve.
https://youtu.(be/mtH1fmUVkfE?t=197) (remove the parentheses)

I was under the impression somewhere in my mind that such a procedure, like the one in video, is also done on employees example to make it look like a bell curve. I had assumed that n=2(5)=10 represents two independent data sets collected by the owner over different periods. The same goes for n=6(5)=30. But original number of employees which is 5 remains the same.

So, I'd say that the question is if in case of n=10 or n=30, the employees number is same as the original, which is 5. Well, it looks like I was wrong because the way author presents it, the number of employees would be 10 when n=10 and 30 when n=30.

It looks like the author is trying to illustrate the idea that a binomial distribution B(n,p) for large N can be approximated by a normal distribution. What precisely does "can be approximated" mean? How would you, or the textbook author do the approximation?

The author only says this, "Let us examine graphically what happens to the binomial distribution when p stays constant but n is increased. Figure 5-6 illustrates the general shape of a family of binomial distributions with a constant p of 0.4 and n’s from 5 to 30. As n increases, the vertical lines not only become more numerous but also tend to bunch up together to form a bell shape. We shall have more to say about this bell shape shortly."

 

[Stephen Tashi]

The author only says this, "Let us examine graphically what happens to the binomial distribution when p stays constant but n is increased. Figure 5-6 illustrates the general shape of a family of binomial distributions with a constant p of 0.4 and n’s from 5 to 30. As n increases, the vertical lines not only become more numerous but also tend to bunch up together to form a bell shape. We shall have more to say about this bell shape shortly."

We'll have to see what the author says later in the text.

I don't know if there is an intuitive way to understand the binomial distribution $B_{2N,p}$ in terms of the binomial distribution $B_{N,p}$. Resorting to algebra we have

$B_{2N,p}(k) = \binom{2N}{k} p^k (1-p)^{2N-k}$

Can we write $B_{2N,p}(k)$ as an expression that is a function of the values of $B_{N,p}$?

 

[PainterGuy]

Thank you!

We'll have to see what the author says later in the text.

I don't think the author is going to say much about it. Perhaps, I was reading too much into it.

I don't know if there is an intuitive way to understand the binomial distribution $B_{2N,p}$ in terms of the binomial distribution $B_{N,p}$. Resorting to algebra we have

$B_{2N,p}(k) = \binom{2N}{k} p^k (1-p)^{2N-k}$

Can we write $B_{2N,p}(k)$ as an expression that is a function of the values of $B_{N,p}$?

I don't see a way.

 

[Stephen Tashi]

The general way to look at things is to consider sums of large number of independent identically distributed random variables. The distribution of such a sum is roughly a bell shaped curve. The "Central Limit Theorem" says this and more.

The binomial distribution B(n,p) is special case of summing independent identically distributed random variables. The binomial distribution B(n,p) can be regarded as the sum of n independent Bernoulli random variables. A Bernoulli random variable $X$ is defined as have the probability density $Pr(X=1) = p ,\ Pr(X=0) = 1-p$.

In your example, the binomial distribution B(5,p) that gives data for 5 employee latenesses can be regarded as summing 5 Bernoulli random variables, one for each of 5 employees. We add 1 to the sum if the employee is late and add zero otherwise.

The general way to look at distribution of the sum of independent random variables is to understand the concept of taking the "convolution" of two distributions. It is correct that a random variable $Y$ that has distribution $B(10,p)$ can expressed in terms of two independent random variables $X_1, X_2$ each of which has distribution $B(5,p)$. The way to do this is $Y = X_1 + X_2$. In your example, this says the data $Y$ from two days of business with 5 employees is computed by adding the lateness data from each of the two days. We get $Y = 4$ in more ways than getting $X_1 =2$ and $X_2= 2$. We also get $Y = 4$ from $X_1 = 0,\ X_2 =4$ and $X_1=1,\ X_2 = 3$, etc. So to compute the probability that $Y = 4$ we must add up the probabilities of all these possibilities. Performing that calculation is called taking the convolution of the distributions of $X_1$ and $X_2$.

 

[PainterGuy]

Thank you very much!

I'm reading on central limit theorem and other topics to get a big picture.

The general way to look at distribution of the sum of independent random variables is to understand the concept of taking the "convolution" of two distributions. It is correct that a random variable $Y$ that has distribution $B(10,p)$ can expressed in terms of two independent random variables $X_1, X_2$ each of which has distribution $B(5,p)$. The way to do this is $Y = X_1 + X_2$. In your example, this says the data $Y$ from two days of business with 5 employees is computed by adding the lateness data from each of the two days. We get $Y = 4$ in more ways than getting $X_1 =2$ and $X_2= 2$. We also get $Y = 4$ from $X_1 = 0,\ X_2 =4$ and $X_1=1,\ X_2 = 3$, etc. So to compute the probability that $Y = 4$ we must add up the probabilities of all these possibilities. Performing that calculation is called taking the convolution of the distributions of $X_1$ and $X_2$.

I understand your comments about convolution and I will try to do it as I get some time.

Can we add up the values individually to get an idea? Let me try.

When n=10, the probability for Y=r=4 is 0.2508 . If I understand you correctly, it means that the following values (r=0, r=4), (r=1, r=3), (r=2, r=2) should be used from the case n=5. I tried to do it three different ways but it didn't work for me. The answer should have been 0.2508. If it's complicated, then no worries. We can get back to it later.

(0.0778*0.0768)+(0.2592*0.2304)+(0.3456*0.3456)= 0.18513
(0.0778+0.0768)+(0.2592+0.2304)+(0.3456+0.3456)= 1. 3354⋅2
(0.0778+0.0768)*(0.2592+0.2304)*(0.3456+0.3456)= 5. 2318×10⁻²

    n = 5; p = 0.4
    B(5,p)

    r        Probability
    0            0.0778
    1            0.2592
    2            0.3456
    3            0.2304
    4            0.0768
    5            0.0102
 

    n = 10; p = 0.4
    B(10,p)

    r        Probability
    0            0.0060 
    1            0.0403 
    2            0.1209 
    3            0.2150 
    4            0.2508     
    5            0.2007
    6            0.1115
    7            0.0425
    8            0.0106
    9            0.0016
    10            0.0001

This question is rather about how 'this' would be done practically. Please check the green highlights; the arrows point those highlights. Link: https://imagizer.imageshack.com/img923/3776/q6Og35.jpg

"Because only five people are involved, the population is too small to be approximated by a normal distribution. We’ll take all of the possible samples of the owners in groups of three, compute the sample means (x_bar), list them, and compute the mean of the sampling distribution (μ_x_bar)."

You can see in Table 6-10, how 10 samples are created each with n=3 from a population with N=5.

"This distribution has a mean of $19,000 and a standard deviation of $2,000. If we draw a random sample of 30 tellers, what is the probability that their earnings will average more than $19,750 annually?"

In Figure 6-8, you see a plot of actual population distribution of bank tellers' earnings and also sampling distribution. My question is how such plots are created in real life.

To keep it simple, I would say that the actual population plot is based on actual database of bank tellers' earnings.

The sampling distribution plot could be created, say, using data of only 30 tellers, and then 'mathematically' a lot of samples could be created with n=25, total samples would be = 30(nCr)25 = 142506. This would give bell shaped distribution which could be approximated using normal distribution.

Do I make sense?

Actually I was reading about the molecular speed distribution when I started this thread. We can see below that population distribution is asymmetric - negatively skewed; it's not normal. I believe that they should have used a label "probability" instead of "number of molecules". I'm focusing on the curve with label "low T".

Total number of molecules = Nm
Number of molecules having certain speed =

Do I have it correct? And is Cp the modal speed? Thanks a lot!

Helpful links:
1: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Map:_Physical_Chemistry_(McQuarrie_and_Simon)/27:_The_Kinetic_Theory_of_Gases/27.3:_The_Distribution_of_Molecular_Speeds_is_Given_by_the_Maxwell-Boltzmann_Distribution
2: https://chem.libretexts.org/Bookshe...ing_Gas_Properties_to_Kinetic_Theory_of_Gases

 

[Stephen Tashi]

When n=10, the probability for Y=r=4 is 0.2508 . If I understand you correctly, it means that the following values (r=0, r=4), (r=1, r=3), (r=2, r=2) should be used from the case n=5.

I don't know what you are denoting by "r". In my notation, one must not only consider the case $X_1=1,\ X_2 = 3$ but also the case $X_1=3,\ X_2 = 1$. So there are more than three probabilities to be added up.

This question is rather about how 'this' would be done practically. Please check the green highlights; the arrows point those highlights. Link: https://imagizer.imageshack.com/img923/3776/q6Og35.jpg

I don't know what you mean by "this".

"Because only five people are involved, the population is too small to be approximated by a normal distribution. We’ll take all of the possible samples of the owners in groups of three, compute the sample means (x_bar), list them, and compute the mean of the sampling distribution (μ_x_bar)."

I don't know what that example is supposed to show. It's a poor choice for showing anything related to the Central Limit Theorem because the central limit theorem deals with samples of identically distributed random variables. To get such a sample of three from a population of 5, you would give each member of the population the same probability of being chosen each time. That allows the possibility that the same member is selected on each of those three times.

The example illustrates "random sampling without replacement". The sampling method relevant to the Central Limit Theorem is "random sampling with replacement".

In Figure 6-8, you see a plot of actual population distribution of bank tellers' earnings and also sampling distribution. My question is how such plots are created in real life.

If there is data for an entire finite population then, in theory, a sampling distribution for the mean value of a sample of size K can be computed by computing the probability for each possible value of that mean. This can be done for random sampling with replacement or for random sampling without replacement.

If the data itself is only a sample from a larger population, then there is no unique answer to your question. People use various ways of estimating the sample distribution.

The sampling distribution plot could be created, say, using data of only 30 tellers, and then 'mathematically' a lot of samples could be created with n=25, total samples would be = 30(nCr)25 = 142506. This would give bell shaped distribution which could be approximated using normal distribution.

You are describing how to create a sampling distribution (for what?) where the sampling method is random sampling without replacement. The resulting curve might be approximately bell shaped. For large populations and small sample sizes, random sampling without replacment gives similar results to random sampling with replacement.

Actually I was reading about the molecular speed distribution when I started this thread.

You'll find it difficult or impossible to interpret statistical physics in the language of mathematical statistics and probability theory.

The develoment of statistical physics preceded modern mathematical probability theory. Statistical physics has its own jargon. Expositions of statistical physics use terminology developed before the modern concept of a probability space. When it comes to defining the set of outcomes, expositions of statistical physics are vague. For example, if a graph shows "The distribution of molecular velocities", mathematical probability theory asks what random variable the distribution describes. Does it refer to selecting a molecule at random from a container of gas? The physical picture is that molecules are colliding and changing velocities, so we don't get a unique velocity by selecting one molecule. We have to pick both a molecule and a specific time. In what finite time interval are we to make the choice?

Instead of thinking of "the distribution of molecular velocities" as a probability distribution, statistical physics tends to view such a graph as the histogram of data for the entire population of molecules. However, there is the difficulty that a given molecule has a changing velocity. So you must pretend that the distribution is a snapshot taken at one instant of time if you want to think of it as being analogous to data about the income of bank tellers.

And is Cp the modal speed?

I think it is, just from looking at the graph.

 

[PainterGuy]

I'm sorry that I couldn't get back to you earlier.

I don't know what that example is supposed to show. It's a poor choice for showing anything related to the Central Limit Theorem because the central limit theorem deals with samples of identically distributed random variables. To get such a sample of three from a population of 5, you would give each member of the population the same probability of being chosen each time. That allows the possibility that the same member is selected on each of those three times.

The example illustrates "random sampling without replacement". The sampling method relevant to the Central Limit Theorem is "random sampling with replacement".

Thank you for pointing this out.

I was thinking of a scenario and not sure if the answer is simple, and if it's not then no need to help me with it! :) Suppose, I'm trying to sample a population of 50 with a sample size 5. I'm trying to sample the population along with another guy; two persons are involved in sampling simultaneously.

If it was only me doing the sampling alone, it would be easy and I could use either 'sampling with replacement' or 'sampling without replacement'. But when sampling is done by both of us, a member from the population is chosen at the same time, wouldn't it create a conflict? How is such a situation is handled in such scenarios and which one of the two, 'sampling with replacement' or 'sampling without replacement', should be chosen as a more practical and sensible methodology?

Note to self:
The combination formula nCr gives you a number of unique combinations without repetition. Use the following formula to find number of combinations with repetition.

1: https://www.statisticshowto.datasciencecentral.com/sampling-with-replacement-without/
2: https://sites.math.northwestern.edu/~mlerma/courses/cs310-05s/notes/dm-gcomb
3: https://keisan.casio.com/exec/system/1223622559

Instead of thinking of "the distribution of molecular velocities" as a probability distribution, statistical physics tends to view such a graph as the histogram of data for the entire population of molecules. However, there is the difficulty that a given molecule has a changing velocity. So you must pretend that the distribution is a snapshot taken at one instant of time

Thank you. Actually, I had a question and also wanted to add more content to complete this topic since it's related to the probability but then I thought it'd better to start a new thread.

I don't know what you are denoting by "r". In my notation, one must not only consider the case $X_1=1,\ X_2 = 3$ but also the case $X_1=3,\ X_2 = 1$. So there are more than three probabilities to be added up.

I'm still struggling with this part. I understand that it's quite frustrating but if it's possible, help me out with this. I'm just curious. In case, you wanted to have a look on the original problem: https://imagizer.imageshack.com/img922/6692/uuUrm0.jpg

"r" is the number of late employees.

You are using Y as a random variable to expresses lateness of of employees from a data set of 10 employees. If Y=4, it'd give you probability of 4 employees being late.

X₁ and X₂ are both random variables expressing the probability of employees being late out of total 5 employees from each data set.

Below I'm going to repeat some parts from earlier posts.

It is correct that a random variable $Y$ that has distribution $B(10,p)$ can expressed in terms of two independent random variables $X_1, X_2$ each of which has distribution $B(5,p)$. The way to do this is $Y = X_1 + X_2$. In your example, this says the data $Y$ from two days of business with 5 employees is computed by adding the lateness data from each of the two days. We get $Y = 4$ in more ways than getting $X_1 =2$ and $X_2= 2$. We also get $Y = 4$ from $X_1 = 0,\ X_2 =4$ and $X_1=1,\ X_2 = 3$, etc. So to compute the probability that $Y = 4$ we must add up the probabilities of all these possibilities. Performing that calculation is called taking the convolution of the distributions of $X_1$ and $X_2$.

Can we add up the values individually to get an idea? Let me try.

When n=10, the probability for Y=4 is 0.2508 . If I understand you correctly, it means that the following values (X₁=0, X₂=4), (X₁=1, X₂=3), (X₁=2, X₂=2) should be used from the case n=5. I tried to do it but it didn't work for me. The answer should have been 0.2508 instead of 1.9796.

(X₁=0 + X₂=4) + (X₁=4 + X₂=0) + (X₁=1 + X₂=3) + (X₁=3 + X₂=1) + (X₁=2 + X₂=2) = (0.0778 + 0.0768) + (0.0768 + 0.0778) + (0.2592 + 0.2304) + (0.2304 + 0.2592) + (0.3456 + 0.3456) = 1. 9796

    n = 5; p = 0.4
    B(5,p)

    r        Probability
    0            0.0778
    1            0.2592
    2            0.3456
    3            0.2304
    4            0.0768
    5            0.0102    n = 10; p = 0.4
    B(10,p)

    r        Probability
    0            0.0060
    1            0.0403
    2            0.1209
    3            0.2150
    4            0.2508    
    5            0.2007
    6            0.1115
    7            0.0425
    8            0.0106
    9            0.0016
    10            0.0001

 

[Stephen Tashi]

. But when sampling is done by both of us, a member from the population is chosen at the same time, wouldn't it create a conflict?

I don't detect a mathematical question in that. It sounds like a question about psychology or sociology.

(X₁=0 + X₂=4) + (X₁=4 + X₂=0) + (X₁=1 + X₂=3) + (X₁=3 + X₂=1) + (X₁=2 + X₂=2) = (0.0778 + 0.0768) + (0.0768 + 0.0778) + (0.2592 + 0.2304) + (0.2304 + 0.2592) + (0.3456 + 0.3456) = 1. 9796

Use notation that distinguishes between an outcome versus the probability of an outcome.
"$X_1 = 0$" is an outcome, not a probability.

Don't use the symbol "+" to mean the word "and". You can use "$\land$" to abbreviate "and".

$Pr( X_1 = 0 \land X_2 = 4) = Pr(X_1 = 0) Pr(X_2 = 4)$, not $Pr(X_1 = 0) + Pr(X_2 = 4)$

 

[PainterGuy]

Thank you! I really appreciate your help.

I don't detect a mathematical question in that. It sounds like a question about psychology or sociology.

I didn't put forward my problem properly so let me try again.

Suppose, I'm trying to sample a population of 50 with a sample size 5. I'm trying to sample the population along with another guy; two persons, A and B, are involved in sampling simultaneously.

If it was only me doing the sampling alone, it would be easy and I could use either 'sampling with replacement' or 'sampling without replacement'. But when sampling is done by both of us, a member from the population is chosen at the same time.

Suppose there is only one "Michael" and "John" in the population of 50, and sampling with replacement is being done.

When John is selected by Person A, the Person B wouldn't have a chance of selected John. The same goes for Michael. This situation would happen for each member of the population.

How is such a situation is handled in such scenarios and which one of the two, 'sampling with replacement' or 'sampling without replacement', should be chosen as a more practical and sensible methodology?

Use notation that distinguishes between an outcome versus the probability of an outcome.
"$X_1 = 0$" is an outcome, not a probability.

Don't use the symbol "+" to mean the word "and". You can use "$\land$" to abbreviate "and".

$Pr( X_1 = 0 \land X_2 = 4) = Pr(X_1 = 0) Pr(X_2 = 4)$, not $Pr(X_1 = 0) + Pr(X_2 = 4)$

I got the correct number now. But how do interpret the result.

In post #11 the following was said.

Initially it was said that n=5 is total number of employees and r is number of late arrivals. If n=10 and r=10, how do these relate to the original number of employees and late arrivals?

Originally, the maximum possible number of late arrivals was 5, as is shown. Assume that the data set was collected over a period of two weeks. Suppose that the owner collects another independent data set over the period of two more weeks. Now there are two independent data sets, each collected separately over the period of 2 weeks, but conveying the same information.

We notice that for n=5, the probability for four late arrivals, i.e. r=4, is 0.0768. But when n=10, the probability for r=4 is 0.2508. The difference is 0.2508 - 0.0768 = 0.174. For n=10, the probability of 4 late arrivals is more.

Complete problem: https://imagizer.imageshack.com/img922/6692/uuUrm0.jpg

In our calculation of Y=4, the probability was found to be 0.25083. Obviously,it provides the probability of 4 employees being late over the period of 4 weeks. What does the case

mean? It'd mean that if you look at the clock-in data of first 2 weeks, and also at the clock-in data of another 2 weeks, the probability of finding total of 7 instances of being late; we can say that n=10 gives us maximum number of instances of being late although the number of employees is still 5. I hope it makes sense.

 

[Stephen Tashi]

How is such a situation is handled in such scenarios

I don't know what you mean specifically by "handled". Are you asking how to compute a sampling distribution?

To talk about a sampling distribution, you must first specified what statistic is being sampled. One can compute statistics from a sample in various ways. For example, from a sample of 5 persons, one could record the height of the tallest of those 5 persons ( an example of "order statistics"). Or one could compute the average height of those 5 persons, or one could compute how many of those 5 persons wear suspenders.

As I understand your example, we have two investigators, I1, I2. They draw a sample of 5 persons from a population of 30 as follows. I1 selects 1 person from the 30. Then I2 selects 1 person from the 29 persons remaining. The the process is repeated on the original population of 30 until each investigator has selected 5 people.

Intuitively, I see no reason why this changes the probability of I2 getting a particular sample. For example assume the persons are designated by numbers 1,2,...30. When I2 does random sampling with replacement by himself there is a certain probability that I2 selects a multi-set such as {1,1,15, 18, 25, }. Does the probability of getting that multi-set change when I1 is picking a person before I2 picks a person?

and which one of the two, 'sampling with replacement' or 'sampling without replacement', should be chosen as a more practical and sensible methodology?

There is no general rule.

I got the correct number now. But how do interpret the result.

The result is $Pr(X_1 + X_2 = 4)$.

In post #11 the following was said.
...

The way you are forming questions in post #``11 is incoherent because it fails to distinguish between the concept of data and the concept of a probability distribution.

In post #``11 you are referring to the collection of data. The calculation you are asking about is done from the values in a probability distribution. To repeat advice from previous posts, a set of data representing samples from a probability distribution is not the same thing as the probability distribution.

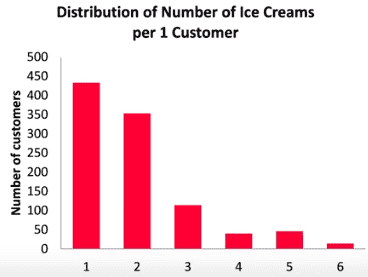
A given binomial distribution such as $B(70,p)$ can be used to model different situations. $B(70,p)$ might model the probability that there are $k$ latenesses among 70 employees on 1 day. It might also model the lateness of 1 employee over a period of 70 days. Or it might model the total latenesses of 5 employees over 14 days.

One interpretation of the probability distribution $B(5,p)$ is that it gives the probability that $k$ employees will be late on 1 given day. The possible values of $k$ are 0,1,2,3,4,5.

If you are talking about 2 weeks of data about lateness , then we consider both $k$ , the number of employees late on a given day and also $d$, the number of days where $k$ employees were late. The possible values of $d$ are 0,1,2,...14. The data concerns the frequency of latenesses. Frequencies are not the same concept as probabilities.

Apparently you are imagining that 2 weeks worth of data are taken and that the data is used to estimate a probability distribution. Ignoring the order of the 14 days, two weeks worth of data can be represented by a set of pairs of numbers of the form $(k,d)$. It might turn out that the data consists of one pair of numbers such as (2,14). Or it might turn out that we need as many as 6 pairs of numbers such as { (0,7),(1,1),(2,1),(3,1)(4,1)(5,3)}. That data could be used to estimate the probability for $k$ employees being late on 1 given day. The procedure for estimation can be done in different ways.If we take $B(5,p)$ as the probability distribution for $k$ employees being late on 1 given day and assume each day is an independent experiment then we can compute the probability distribution for x total lateness in D total days. This done by taking the "D-fold convolution" of $B(5,p)$. Because of the special nature of the binomial distribution, the D-fold convolution of $B(5,p)$ is $B(5D,p)$. Those calculations have nothing to do with specific data.

The binomial distribution is special. Let $f(K)$ be a non-binomial distribution for the probability that $k = 0,1,2,..K$ employees are late on a 1 given day. It is not, in general, true that the D-fold convolution of $f(K)$ is $f(KD)$. Constraints about the total number of employees and the total number of days might be critical if we use a non-binomial distribution to model what happens on 1 day.