Questions involving more than one voltage source

[dimpledur]

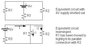
Consider the following circuit.

Using superposition determine a) the magnitude and b) the direction of the current going through R_1 (is it away from node a?). Dtermine the c) magnitude and d) direction of the current through R_2 (is it away from node b?). e) Find V_{ab}.

a) First, I will find the equivalent resitance, and then short each of the voltage supplies and determine the current separately.

R_{eq}=4\Omega+[(1/3\Omega)+(1/5\Omega)]^{-1}=5.875\Omega

I_{R_{1,1}}=(R_{eq})(R_{1})^{-1}(I_1)

I_{R_{1,1}}=(5.875\Omega)(4\Omega)^{-1}(4V/5.875\Omega)=1 A away from node a.

Due to the other voltage source, we have I_{R_{1,2}}=(R_{eq})(R_{1})^{-1}(I_2)

I_{R_{1,2}}=(5.875\Omega)(4\Omega)^{-1}(6V/5.875\Omega)=1.5 A towards node a.

Therefore, the magnitude of the current going through I_{R_1}=1.5A-1A=0.5A. For b) it is directed towards a.

Next, this is where I get rather confused, and because of the ground location.. Let's say for a minute that the current goes through R1 and heads towards R2, what is stopping it from going through the ground rather than the resistor? Anyways, here is my attempt.

R_{eq}=5.875\Omega

I_{R_{2,1}}=(R_{eq})(R_{2})^{-1}(I_1)

I_{R_{2,1}}=(5.875\Omega)(5\Omega)^{-1}(4V/5.875\Omega)=0.8 A away from node b.

Due to the other voltage source, we have I_{R_{2,2}}=(R_{eq})(R_{2})^{-1}(I_2)

I_{R_{2,2}}=(5.875\Omega)(5\Omega)^{-1}(6V/5.875\Omega)=1.2 A[/tex away from b.<br /> <br /> c) 1.2 A+ 0.8A= 2 A d) away from b.<br /> <br /> e) I find this one very confusing too. V_{ab} = V_a-V_b=1.915V-1.277V=0.638V

 

[gneill]

Your Req is the equivalent resistance seen by the 4V battery. So the current it produces is 4V/Req. From the circuit you can see that it is also its superposition contribution to the current through R1.

For the contribution of the 6V battery, if I may suggest, turn the 6V battery along with R2 and R3 into a Norton equivalent. That'll place it in parallel with R1 (when the 4V battery is removed), so it's a simple current division problem at that point.

 

[dimpledur]

I haven't been exposed to Norton equivalents yet, however, would you say combining resistor 3-olm and 5-olm would be suffice tomake the circuit as an entirety in series? For example, in series we would have the 4V battery, the 6 V battery facing opposite direction, R1, and of course [(1/3)+(1/5)]^-1 =2-olm resistor underneath the 6 volt battery.

 

[gneill]

I haven't been exposed to Norton equivalents yet, however, would you say combining resistor 3-olm and 5-olm would be suffice tomake the circuit as an entirety in series? For example, in series we would have the 4V battery, the 6 V battery facing opposite direction, R1, and of course [(1/3)+(1/5)]^-1 =2-olm resistor underneath the 6 volt battery.

No, because R2 and R3 (5Ω and 3Ω) are not in parallel -- the 6V battery is "in the way" of a parallel connection of those two resistors.

However, if you're using superposition, when you remove one source at a time you may find "opportunities" to have certain resistances in parallel. When the 6V battery is removed (shorted) to determine the contribution of the 4V battery to the current through R1, then R2 and R3 appear in parallel. On the other hand, when the 4V battery is removed, R2 and R1 appear to be in parallel.

 

[dimpledur]

Alright, I believe I have it.

For the 4 V battery, Req= 4 + [(1/3)+(1/5)]^{-1} = 5.875-olm and thus I=4/5.875=0.681 A away from a.

For the 6 V source, Req= [(1/8)+(1/4)]^{-1} =2.67-olm. The total current is 6 V/2.666=2.25 A, and we can now apply current divider to find the current through R1.
I1=(2.67/4)(2.25)= 1.50 A towards a.

Total is 1.5-0.681=0.819 A towards node a. Does that look right?

 

[gneill]

The 4V battery calculation looks fine. The 6V calculation needs a re-think. Try redrawing the circuit when the 4V battery is removed, moving R1 to the left vertical position (where the 4V battery was) and R2 to the right vertical position (ignore the ground indicator at b for now). What's in parallel?

 

[dimpledur]

Oh right, everything is!

 

[dimpledur]

Okay, Req=[(1/4)+(1/5)+(1/3)]^-1=1.277-olm

Is=6V/1.277=4.7 A

now, through the 4 olm resistor we have:
I=(1.277/4)(4.7)=1.5? Thats weird

 

[gneill]

Well, you have three parallel branches anyways. One branch contains the series connection of R3 and the 6V battery. But I think you can see how R1 and R2 are in parallel, and you can work from there. Either find the voltage across the R1||R2 pair and then the current through R1, or find the total current provided by the 6V battery through the equivalent resistance and then current-divide it through the R1||R2 pair. Your choice.

 

[dimpledur]

Alright, thanks for your help! I am done for the day lol

 

[dimpledur]

Wait, just a quick question regarding Vab, essentially I want to find the voltage due to the 6V battery on R1, and that will equal its contribution at point a. Then I would a 4 V to that value to find the total Va? Also, Vb=0 since it is the reference?

 

[gneill]

Once you have the total current through R1 you can calculate the voltage across it. What are the two end points of R1?

Here's a couple of diagrams that might help to visualize what we've been trying to accomplish with the 6V battery contribution.

 

[dimpledur]

Sweet, then Vab is simply total current*4-olm. THX!