Quick Question about Pendulum Graphs

[Abu]

Hi everyone. I just have a very quick question regarding position time graphs and velocity time graphs for a pendulum.

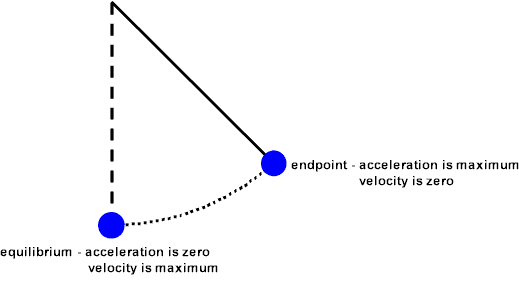
As we know, at the maximum displacement, the acceleration is at its maximum and the velocity is zero, and vice versa when the displacement is zero.

When we put this information on a velocity time graph, it looks like this:

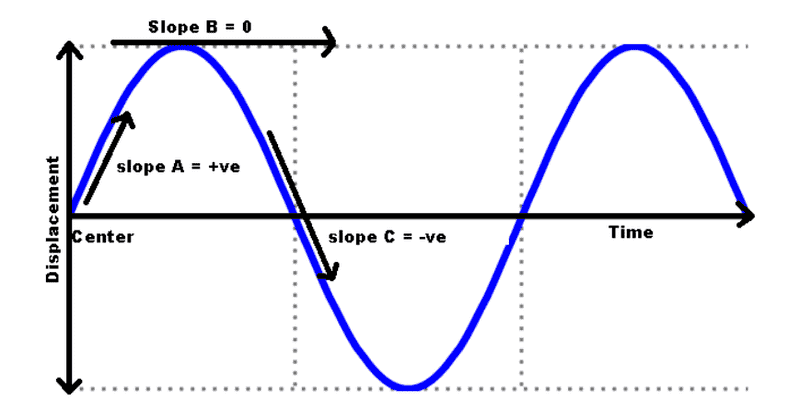
When we have curved lines on a velocity time graph, as seen above, this means that there is increasing and decreasing acceleration, correct? Specifically, that means that the value of the acceleration itself is decreasing or increasing (for example, 10 m/s^2, 8 m/s^2, 5 m/s^2).

This information put onto a position time graph looks something like this:

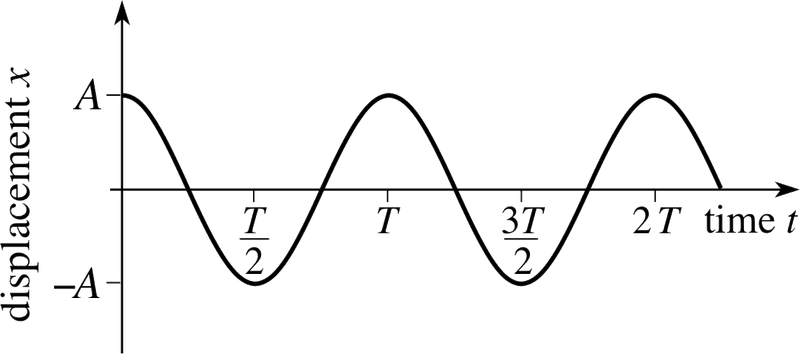
As we can see, there is once again curved lines. However, on a position or displacement time graph, these curved lines don't mean increasing acceleration or decreasing acceleration like they do for the velocity time graph, but instead they mean constant acceleration or constant deceleration.

So how can the displacement time graph use curved lines? It implies that the acceleration is a constant number that doesn't change, which is obviously not true as we see that the acceleration is zero at 0 displacement and the acceleration is at it's maximum value at the largest displacement, so obviously there must be a change, not constant.

I hope my question makes sense, thank you all for your patience.

 

[Doc Al]

As we can see, there is once again curved lines. However, on a position or displacement time graph, these curved lines don't mean increasing acceleration or decreasing acceleration like they do for the velocity time graph, but instead they mean constant acceleration or constant deceleration.

So how can the displacement time graph use curved lines? It implies that the acceleration is a constant number that doesn't change, which is obviously not true as we see that the acceleration is zero at 0 displacement and the acceleration is at it's maximum value at the largest displacement, so obviously there must be a change, not constant.

Why in the world do you think that curved lines on a displacement vs time graph imply constant acceleration?

 

[Abu]

Why in the world do you think that curved lines on a displacement vs time graph imply constant acceleration?

Sorry, it's just what I've been taught in class. I was told that those curved lines on a displacement time graph would imply a constant acceleration or constant deceleration. I'm assuming that is wrong?

What would constant acceleration look like on a displacement-time graph, then? Or what does increasing/decreasing acceleration look like?

Thank you for your response and time.

 

[lekh2003]

When we have curved lines on a velocity time graph, as seen above, this means that there is increasing and decreasing acceleration, correct? Specifically, that means that the value of the acceleration itself is decreasing or increasing (for example, 10 m/s^2, 8 m/s^2, 5 m/s^2).

No, just think about this. Acceleration should always be constant, gravity is not changing it's force along the path of the pendulum. What's changing is the velocity here. That's why its a velocity graph.

As we can see, there is once again curved lines. However, on a position or displacement time graph, these curved lines don't mean increasing acceleration or decreasing acceleration like they do for the velocity time graph, but instead they mean constant acceleration or constant deceleration.

So how can the displacement time graph use curved lines? It implies that the acceleration is a constant number that doesn't change, which is obviously not true as we see that the acceleration is zero at 0 displacement and the acceleration is at it's maximum value at the largest displacement, so obviously there must be a change, not constant.

I do not understand what you are saying here.

Sorry, it's just what I've been taught in class. I was told that those curved lines on a displacement time graph would imply a constant acceleration or constant deceleration. I'm assuming that is wrong?

You are obviously very confused, go back to your teacher and discuss it with them and ask them to explain what they might have said in class.

 

[Doc Al]

Sorry, it's just what I've been taught in class. I was told that those curved lines on a displacement time graph would imply a constant acceleration or constant deceleration. I'm assuming that is wrong?

Yes, that is wrong. I suspect (and hope!) that you've just misheard what your teacher was saying in class. It's true that if something has a constant acceleration, then its displacement over time graph would be curved, but that does not mean that any curved displacement graph means constant acceleration.

What would constant acceleration look like on a displacement-time graph, then?

A good example of constant acceleration would be a falling object. Imagine tossing something straight up into the air. What would its displacement versus time graph look like?

Something like this:

When you examine a displacement - time graph, consider the slope of the graph at any point. (The slope of the line tangent to the graph at any point.) That slope describes the velocity at that point. In the above graph, the velocity (and thus the slope) starts out high and positive, keeps getting lower until at the top the velocity is momentarily zero, and then starts picking up speed as the object comes down (the velocity -- slope -- is negative). Given that, what would the velocity graph look like?

Something like this:

Note that the velocity graph is a straight line. (Unlike your pendulum motion example.) And the slope of the velocity graph gives the acceleration, which for a projectile is a constant (and negative).

Or what does increasing/decreasing acceleration look like?

In the case of the pendulum motion, the acceleration is not constant. It turns out that a graph of the acceleration versus time would also be sinusoidal, just like the displacement graph.

 

[Doc Al]

Acceleration should always be constant, gravity is not changing it's force along the path of the pendulum. What's changing is the velocity here.

While gravity is constant, the string also exerts a force on the pendulum. The tangential acceleration, which is what is being described here, is not constant.

 

[lekh2003]

While gravity is constant, the string also exerts a force on the pendulum. The tangential acceleration, which is what is being described here, is not constant.

Ahh, ok. I was mistaken.

 

[Abu]

Yes, that is wrong. I suspect (and hope!) that you've just misheard what your teacher was saying in class. It's true that if something has a constant acceleration, then its displacement over time graph would be curved, but that does not mean that any curved displacement graph means constant acceleration.A good example of constant acceleration would be a falling object. Imagine tossing something straight up into the air. What would its displacement versus time graph look like?

Something like this:
View attachment 217955
When you examine a displacement - time graph, consider the slope of the graph at any point. (The slope of the line tangent to the graph at any point.) That slope describes the velocity at that point. In the above graph, the velocity (and thus the slope) starts out high and positive, keeps getting lower until at the top the velocity is momentarily zero, and then starts picking up speed as the object comes down (the velocity -- slope -- is negative). Given that, what would the velocity graph look like?

Something like this:
View attachment 217956

Note that the velocity graph is a straight line. (Unlike your pendulum motion example.) And the slope of the velocity graph gives the acceleration, which for a projectile is a constant (and negative).

In the case of the pendulum motion, the acceleration is not constant. It turns out that a graph of the acceleration versus time would also be sinusoidal, just like the displacement graph.

Ah okay, thank you so much for your reply.

So it isn't necessarily wrong to say that a curved line on a displacement time graph represents constant acceleration or constant deceleration, but in some cases that curved line could mean an increasing or decreasing acceleration instead, right? I'm guessing the two variations would like pretty similar?

By the way, thank you very much for the effort and time you put into helping me, I really appreciate it.

 

[Doc Al]

So it isn't necessarily wrong to say that a curved line on a displacement time graph represents constant acceleration or constant deceleration, but in some cases that curved line could mean an increasing or decreasing acceleration instead, right?

I would put it more simply: A curved line on a displacement time graph implies some kind of acceleration (since the velocity is changing), but whether that acceleration is constant or changing depends on the details of that graph.

I'm guessing the two variations would like pretty similar?

In the projectile motion case, the displacement time graph is a parabola, but in the pendulum case the graph is sinusoidal. Those graphs look pretty different to me!