On Bodies Moving with a Constant Velocity

[JackFyre]

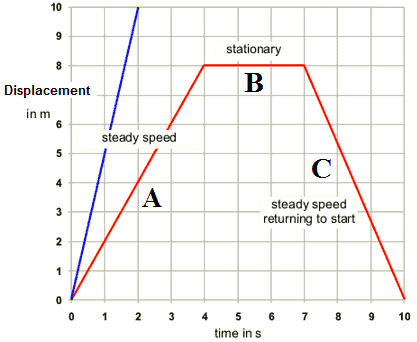
Is the below Displacement time graph posible?
if an object is in motion at a constant velocity, is it possible for it to stop instantaneously, or does there have to be a decelaration?
According to Newton's first, an object will remain in its state of constant velocity unless acted upon by external forces. Here, our object has a constant velocity, but then it stops; therefore, there has to be an external force. Now, if there IS an external force, there would be an acceleration, which would result in a curve in the S-T graph.
but there is no curve... So is that possible?

 

[Delta2]

Strictly speaking this graph is not possible.
However if we assume that the acceleration (or deceleration ) that is applied is very big so that the time interval to bring it to a full stop (or to some velocity $v_0$) is negligibly small so we can omit this time interval (and the corresponding curve) in the graph. SO we can say at the end of day that this graph is approximately correct when all the necessary accelerations (or decelerations) are big enough.

 

[Ibix]

Strictly, no. An infinite force would be required. However, it's common to approximate very brief accelerations this way. Imagine a child's toy car running into a wall. It will come to a dead stop in a fraction of a millisecond, which is too short to show up on your graph. Neglecting this phase makes almost no difference and makes the maths a lot easier.

 

[JackFyre]

I get it. Thanks folks.
Based on your responses, can I conclude that these kinds of graphs cannot represent any physical body in reality, that is they are wrong; but can be considered accurate for all practical purposes.

 

[Ibix]

A question: if the acceleration phase lasted a millisecond, how different would that graph look versus instantaneous acceleration? If it wouldn't be measurably different, how can it be wrong?

It's important to realize that neglecting effects that are indetectable doesn't make your answers wrong, it just means that the model you are using has a limited range of validity. In this case, with a high enough speed camera you would be able to record the acceleration phase, but you don't have that time resolution here. This comes up time and time again in physics, which is why I'm going on about it. For example, NASA uses Newtonian gravity instead of general relativity to send probes around the solar system because the errors from doing so are too small to matter (unpredictable micrometeoroid impacts are far more significant), but you can see errors from neglecting relativity if you study planetary motion carefully enough.

Isaac Asimov's short essay https://chem.tufts.edu/answersinscience/relativityofwrong.htm is worth a read.

 

[Delta2]

I get it. Thanks folks.
Based on your responses, can I conclude that these kinds of graphs cannot represent any physical body in reality, that is they are wrong; but can be considered accurate for all practical purposes.

Yes strictly speaking they are wrong, however they are a very good approximation. In physics we do approximations all the time, the most widely used approximation is that of gravitational acceleration $g$ that we consider it to be constant for small (in comparison to the radius of Earth $R=6400km$) height $h$ over the surface of earth, while in fact it isn't constant, it varies as of $\frac{1}{(R+h)^2}$.

 

[A.T.]

can I conclude that these kinds of graphs cannot represent any physical body in reality, that is they are wrong;

Note that such a graph doesn't have to represent a massive body, it could be some geometrically constructed point, that doesn't require infinite forces for infinite accelerations.

... but can be considered accurate for all practical purposes.

Graphs usually have limited precision anyway. As long as the physical inaccuracy is less than the graph precision, it is of no concern.

Finally, as others mentioned, all descriptions in physics are idealizations of the real world.

 

[jbriggs444]

Judging by the thickness of the red line, that graph is only accurate to about +/- 5 cm and +/- 50 ms anyway.

 

[JackFyre]

"Judging by the thickness of the red line, that graph is only accurate to about +/- 5 cm and +/- 50 ms anyway. "
I think the thickness of the line is unavoidable, because we can safely assume that it represents an imaginary line of no thickness. My problem with the graph is not that its 'inaccurate'. It is pretty accurate, as put forth by all of you, and I agree with that. My problem is that it gives the wrong message.
In my opinion, this particular thing must be mentioned beneath the graph, otherwise graphs like these can easily mislead someone into believing that a change in velocity can occur instantaneously; i.e, without the 'curve' in the graph. But this notion totally undermines the whole of Newtonian mechanics, and can injure a student's understanding of its fundamentals.
I do hope I'm clear!

 

[russ_watters]

My problem with the graph is not that its 'inaccurate'. It is pretty accurate, as put forth by all of you, and I agree with that. My problem is that it gives the wrong message.
In my opinion, this particular thing must be mentioned beneath the graph, otherwise graphs like these can easily mislead someone into believing that a change in velocity can occur instantaneously; i.e, without the 'curve' in the graph. But this notion totally undermines the whole of Newtonian mechanics, and can injure a student's understanding of its fundamentals.

Where did you get the graph? What is the context? How it is presented matters a lot for whether it sends a right or wrong message. Heck, this is the first time the word "student" has appeared in the thread...

 

[A.T.]

In my opinion, this particular thing must be mentioned beneath the graph, otherwise graphs like these can easily mislead someone into believing that a change in velocity can occur instantaneously; i.e, without the 'curve' in the graph. But this notion totally undermines the whole of Newtonian mechanics, and can injure a student's understanding of its fundamentals.

As a student I was happy to get a simplified graph, because the math is easier. Not every problem asks to calculate forces.

 

[vanhees71]

For me the greatest relieve was when I learned Hamilton's principle and I had not to use forces anymore to get equations of motion ;-)).

But now to the problem. The graph in #1 is obviously oversimplified. You can nevertheless formally calculate the forces needed to produce such a space-time diagram. There's of course no force in all points where the velocity is constant (Newton's Lex II). Now take the situation close to $t=4 \; \text{s}$. You can describe the motion as
$$x(t)=v t \Theta(t-t_0)+v t_0 \Theta(t_0-t), \quad t \in [0,7 \text{s}].$$
Then you get
$$\dot{x}(t)=v \Theta(t-t_0) + v t \delta (t-t_0) -v t_0 \delta(t-t_0) = v \Theta(t-t_0).$$
Since $v=\text{const}$ from this we get
$$\ddot{x}(t)=a(t)=v \delta(t-t_0),$$
i.e., the idealized spacetime diagram implies a $\delta$-distribution force $F=m a$ at time $t_0=4 \; \text{s}$, which of course doesn't exist in reality. It's just a simplified model for a short impuls, neglecting the duration of that impulse.