Radius of a circle that intersects two points on a right triangle.

[dgoldman86]

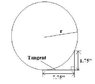
Homework Statement

I'm trying to figure out the radius of a circle that intersects two points on a right triangle. One side of the triangle is tangent to the circle and the other intersects it. I have attached an image that helps further explain what I'm talking about. Knowing what I have listed in the image is there anyway to determine the radius of that circle?

 

[Dick]

If you think about it in terms of coordinates and represent the circle by the equation x^2+y^2=r^2, then then tangent vertex on your triangle is (0,-r), right so far? What are the coordinates of the other vertex on the circle? It must also have a distance from the center of the circle at (0,0) of r, yes? That should give you an equation to solve for r.

 

[Mentallic]

You could also go about solving this without using coordinate geometry.
Draw a hypotenuse for that right angled triangle, which will have a length of \sqrt{x^2+y^2} and then draw two radii connecting to each end of the triangle, ofcourse these will both have length r since they're radii.
Now label the angle between the two radii as \theta, do you know what the length of \sqrt{x^2+y^2} is in terms of r and \theta?

Once you find that out, you'll have an equation in terms of r and \theta, and since we don't know the second variable, we'll need to find one more equation. Consider the properties of the side of the triangle that is tangent to the circle.

p.s. Is it just me or has LaTeX changed?

 

[Dick]

No not just you. There is something funky going on with LaTeX lately.

 

[Saitama]

name the vertex as shown in the picture below.

Join AC.
In right triangle ABC,
\sqrt{(1.75cm)^2 + (7.75cm)^2} = 7.95cm

Now draw a perpendicular OD to AC.
Since perpendicular drawn from the centre of a circle to a chord bisects the chord. Therefore AD=CD=3.975cm.

In triangle ABC,
tan \theta = 1.75/7.75

tan \theta = 0.225

\theta = tan_-1 0.225

\theta = 12.68 degrees

Now join OC.
Since BC is a tangent, therefore Angle OCD = 90 - 12.68 = 77.32 degrees

in triangle OCD,
cos 77.32 degrees = 3.975/OC
0.22 = 3.975cm/OC
OC = 18.07 cm

Since OC = radius of circle
Therefore radius of circle = 18.07 cm

(Please someone correct it if it is wrong).

 

[Saitama]

I don't understand why Theta doesn't come in line with tan.
Please someone tell me how to correct this out, I am new to the board...

 

[Mentallic]

I don't understand why Theta doesn't come in line with tan.
Please someone tell me how to correct this out, I am new to the board...

It probably has something to do with:

No not just you. There is something funky going on with LaTeX lately.

Notice the LaTeX used in my post, I didn't intend to have it on a new line but it decided to do that, so when you put tan in normal text and then theta in LaTeX, it jumped a line.

Also, please don't give out full solutions - it's part of the forum rules.

And the final formula is \frac{\sqrt{x^2+y^2}}{2tan^{-1}\left(\frac{y}{x}\right)}
where x<y<r

And plugging in those values given, I get 17.89 rounded off. Your answer is probably slightly off due to your intermediate rounding.

 

[Saitama]

Thanks Mentallic for notifying me.
I will keep care of it...

 

[dgoldman86]

Thank you. All of this was very helpful.