- #1
hawaiidude
- 41
- 0
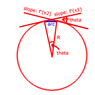
how do you calculate the radius of curvature and the center p(h,k) of the circle with respect to the curve and how do you do improper integrals? kinda forgot improper integrals.