NEGATIVE_40
- 22
- 0
Homework Statement
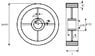
What is the radius of gyration (in meters) for the steel flywheel shown? The width of its rim, L, is as given below. The density of steel is 7500 kg/m3. The outside diameter (OD)for the wheel is 2000 mm, and the inside diameter (ID) is 1840 mm as shown in the figure. The spokes are of cylindirical cross section with the diameter 70 mm. The hub OD and ID are 400 mm and 200 mm, respectively. The hub width is half of the rim width.
*see attachment for diagram*
Homework Equations
k= \sqrt{\frac{I}{m}}, where k is the radius of gyration, I is the moment of inertia and m is the mass
I_x=\frac{1}{4} mR^2 for a thin disk (I used the formula for circular cylinder initially, but it just reduced to this anyway)
I_y= \frac{1}{12}m(3R^2+l^2) +m \bar{y}^2 for circular cylinder, in my case it is for the vertical spokes.
The Attempt at a Solution
I started by finding the total mass of the flywheel, and I am fairly sure I have that part correct
The part where I think I am making my mistake is in calculating the moments of inertia.
for the circular bits
I_x =\frac{m_{big~circular ~bit}}{4}(R_{BO}^2-R_{Bi}^2)+ \frac{m_{little~circular~bit}}{4}(R_{SO}^2-R_{Si}^2)
then for the horizontal spokes:
I_{x, horizontal spokes} = 2*\left [ \frac{1}{2}m_{one~spoke}R^2 \right ] where R is the radius of the spoke.
for the vertical spokes using parallel axis theorem:
I_{x, vertical spokes} = 2*\left [ \frac{1}{12}m_{one~spoke}(3R^2+l^2) +m_{one~spoke} \bar{y}^2 \right ]
I've then added all of these moments of inertia together and used
k= \sqrt{\frac{I}{m}}
but my answer is wrong.
Have I missed anything in my working, or used the wrong inertia formula somewhere?
Am I supposed to take the moment of inertia about the x – axis in this case? (would it make a difference if I did it about another axis?)
This question has really got me confused, so any help would be appreciated!
Attachments
Last edited: