Range of y: Solving Exercises with x=0

[SamitC]

Hello,
This is a very basic question but bothering me on some exercises.

,

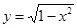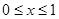
Then how is the range of y is

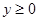? What if x is 0, then we can have y = 1 or y = -1.
While doing some exercises I encountered this issue and can't match the answers.
Thanks in advance

 

[.Scott]

For the most part, $\sqrt{x}$ indicates the positive square root value.

Since, in this case, y is a function, there is not the slightest ambiguity. Functions are only allowed to have one value for anyone input. So $y=\sqrt{1-x^2}$ refers only to the positive root.

 

[fresh_42]

If you just write $y = \sqrt{1-x^2}$ then it is only the positive root. Otherwise you should write $y = ± \sqrt{1-x^2}$ to indicate that you consider both roots. And even this is a bit sloppy because it means $y \in \{ ± \sqrt{1-x^2} \}$. I normally write $y_{1,2} = ± \sqrt{1-x^2}$.

 

[SamitC]

For the most part, $\sqrt{x}$ indicates the positive square root value.

Since, in this case, y is a function, there is not the slightest ambiguity. Functions are only allowed to have one value for anyone input. So $y=\sqrt{1-x^2}$ refers only to the positive root.

The function part made it clear. Thanks.

 

[Erland]

But the range isn't $y\ge 0$. It's $0\le y\le 1$.