Ineedhelpwithphysics
- 43
- 7
- Homework Statement
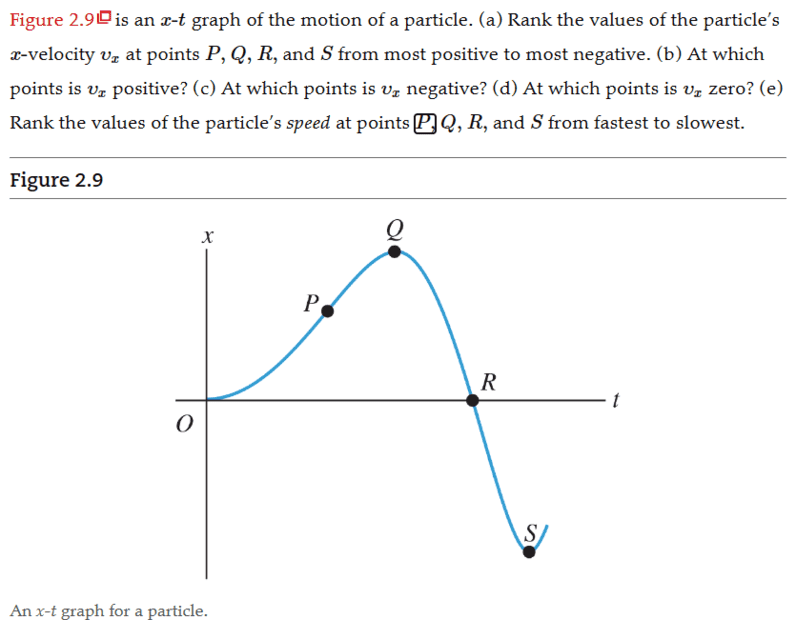
- (E) Rank the values of the particles speed at points P, Q, R, S from fastest to slowest
- Relevant Equations
- Speed = distance/time
My answer is R > P > Q = S
Since R is more steeper than P the speed is greater, speed is a non-negative unit so i assume that speed of R will be greater than P
Speed of P has a positive slope, also the magnitude is positive.
Q and S are the same due to the fast that they both horizontal slopes which means the object is not moving which means no speed.
This is my work , correct me if i'm wrong, thanks ^^^
Since R is more steeper than P the speed is greater, speed is a non-negative unit so i assume that speed of R will be greater than P
Speed of P has a positive slope, also the magnitude is positive.
Q and S are the same due to the fast that they both horizontal slopes which means the object is not moving which means no speed.
This is my work , correct me if i'm wrong, thanks ^^^