Ray Optics: Examining Meter Stick in Tank

[rayhan619]

Homework Statement

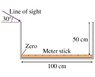
The figure shows a meter stick lying on the bottom of a 100-cm-long tank with its zero mark against the left edge. You look into the tank at a 30^\circ angle, with your line of sight just grazing the upper left edge of the tank.
1)What mark do you see on the meter stick if the tank is empty?
2)What mark do you see on the meter stick if the tank is half full of water?
3)What mark do you see on the meter stick if the tank is completely full of water?

Homework Equations

The Attempt at a Solution

 

[LowlyPion]

Welcome to PF.

What are your thoughts on how to solve the problem?

 

[rayhan619]

im not sure how to start this problem. please help me

 

[Delphi51]

Sketch a ray originating at some point on the meter stick, going up the surface at an angle, refracting to a larger/smaller angle as it emerges from the water.

That was just for practise. Now draw a similar ray that goes right into the observer's eye from point x on the ruler. Use the law of refraction to work back from the angle of refraction to the x on the ruler.

 

[rayhan619]

i get x = 42.9 cm.
is it right?
how do i do part b and c.
i have attached the picture

 

[Delphi51]

I can't actually do the problem without knowing the height of the tank and I don't understand "a 30^\circ angle".

 

[rayhan619]

i have attached the picture in my previous post. i guess the height is 50 cm. and "a 30^\circ angle" means a 30 degree angle
thank you

 

[Delphi51]

The a part has no refraction - the ray is a straight line at 30 degrees to the bottom of the tank. Tan(30) = 50/x When you solve that for x, I don't think you get 42.9. It would have to be greater than 50.

For part (b) - half full - you must do a Law of Refraction formula to see how the angle changes. See http://en.wikipedia.org/wiki/Refraction
Look up the index of refraction for water and for air to put in the formula. Show your work here if you would like a check.

 

[rayhan619]

a) tan(30) = 50/x
x = 50/tan(30)
x= 86.6

b) n1 sin(theta1) = n2 sin (theta2)
theta1 = sin^-1 (sin 60*1.00/1.33)
theta1 = 40.63

tan(40.63) = x/50
x = tan (40.63) * 50
x = 42.9

c) is it same as b?
whats the difference between half full and full?

 

[rayhan619]

i got a and c right, but not sure how to do part b.

 

[Delphi51]

(b) is a bit more complicated because the ray travels at the original angle until it hits the water. You'll have to find the horizontal part of that and add it to the horizontal part traveled at the 40.6 degrees to get the total x. A diagram will be essential!