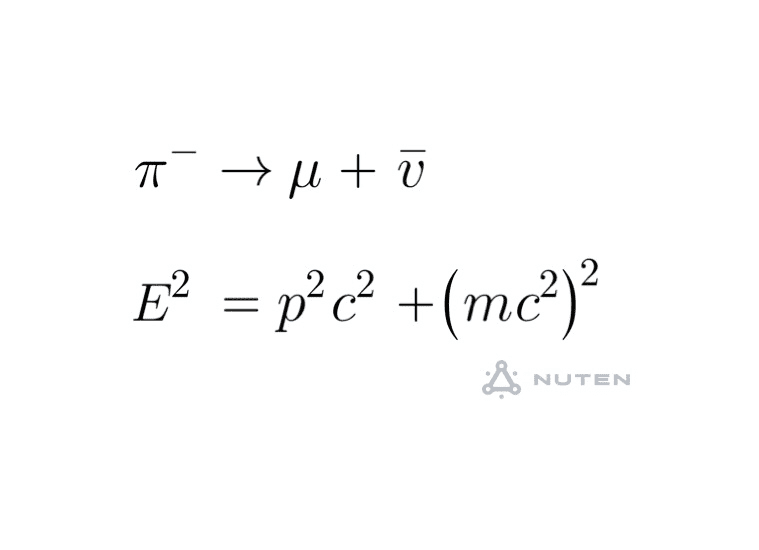Reacting to Life's Changes: Tips for Coping

[jjson775]

Homework Statement

A pion at rest (m = 270 me) decays to a muon (m = 206 me), and an anti neutrino (mv = apx. 0). See reaction below. Find the kinetic energy of the muon and the anti neutrino in electron volts. Hint: relativistic momentum is conserved.

Relevant Equations

See below

Reaction:

 

[kuruman]

Homework Statement:: A pion at rest (m = 270 me) decays to a muon (m = 206 me), and an anti neutrino (mv = apx. 0). See reaction below. Find the kinetic energy of the muon and the anti neutrino in electron volts. Hint: relativistic momentum is conserved.
Relevant Equations:: See below

Reaction:
View attachment 277476View attachment 277477

It took me a while to decipher mv = apx. 0 as $m_{\nu}\approx 0$. More importantly, I don't see the two necessary conservation equations. Plese repost them using symbols, not numbers, for each known and unknown quantity.

 

[PeroK]

Homework Statement:: A pion at rest (m = 270 me) decays to a muon (m = 206 me), and an anti neutrino (mv = apx. 0). See reaction below.

Particle masses are given in $MeV$ because this is simpler than using $kg$. There's no reason to convert to $kg$.

 

[kuruman]

Particle masses are given in $MeV$ because this is simpler than using $kg$. There's no reason to convert to $kg$.

I think "me" stands for "electron mass", $m_e.$

 

[jjson775]

It took me a while to decipher mv = apx. 0 as $m_{\nu}\approx 0$. More importantly, I don't see the two necessary conservation equations. Plese repost them using symbols, not numbers, for each known and unknown quantity.

I don’t have any way to put symbols into either the Homework Statement or Relevant Equations using my iPad. Physics Forum does not allow cut and paste into these spaces. I have to input symbols with my Nuten app then paste into the “Work” space. What conservation equations do you men?

 

[PeroK]

What conservation equations do you men?

Energy & momentum. What else?

 

[kuruman]

I don’t have any way to put symbols into either the Homework Statement or Relevant Equations using my iPad. Physics Forum does not allow cut and paste into these spaces. I have to input symbols with my Nuten app then paste into the “Work” space. What conservation equations do you men?

Perhaps you can use LaTeX which is easy to learn. Just click (tap) LaTeX Guide, lower left just above "Attach files" on this screen for a quick guide.

 

[jjson775]

Perhaps you can use LaTeX which is easy to learn. Just click (tap) LaTeX Guide, lower left just above "Attach files" on this screen for a quick guide.

The guide says you can only display raw code using iOS. I think Nuten will work better for me but will have to be careful with the homework statement.

 

[jjson775]

Energy & momentum. What else?

I think "me" stands for "electron mass", $m_e.$

Correct. Sorry for the lack of subscript.

 

[jjson775]

Energy & momentum. What else?

in the photo of my work, just below the table, I believe both these are addressed. pu = pv(bar) implies conservation of momentum since the pion is at rest and the momenta of the recoiling particles must equal each other.

 

[PeroK]

in the photo of my work, just below the table, I believe both these are addressed. pu = pv(bar) implies conservation of momentum since the pion is at rest and the momenta of the recoiling particles must equal each other.

My suggestion is to use $M$ for the Pion and $m$ for the muon and use Latex. E.g. $$E^2 = p^2c^2 + m^2 c^4$$
Now, what about writing down the consefvations laws (without the numbers in kg).

 

[jjson775]

This is how I showed momentum and energy in the photo of my work.

 

[PeroK]

This is how I showed momentum and energy in the photo of my work.

I'm not convinced you have much idea of how to solve this problem. Are you self-studying SR? Have you not seen material on particle decays and energy-momentum relations?

 

[kuruman]

1612578162016.png

This is how I showed momentum and energy in the photo of my work.

Look, the idea behind any conservation equation is that the conserved quantity before an event happens is the same after the event happens. This in itself doesn't say much, but if you can find ways to rewrite the "before" and "after" conserved quantity in terms of given variables, you are in business. I will get you started with the energy conservation equation.

First you write (as silly as it may sound) the energy conservation equation as $$E_{\text{before}}=E_{\text{after}}$$Then you decide what the "event" is. Here the event is a pion decaying from rest. Before the decay, you only have a pion. Obviously then $E_{\text{before}} = E_{\pi}$ where $E_{\pi}$ stands for "the energy of a pion at rest".

Next you look at the energy after and do the same thing. What do have after the decay? Answer: A neutrino and a muon. Obviously then $E_{\text{after}} = E_{\mu}+ E_{\nu}$ where $E_{\mu}$ and $E_{\nu}$ stand, respectively, for the energy of the muon and the energy of the neutrino.

Therefore the energy conservation equation can be transformed to $$ E_{\pi}=E_{\mu}+ E_{\nu}.$$The third step is rewriting the total energies of each particle. What is the relativistic total energy of a particle? Apply that to what you have here. In your attempt you wrote

$E_{\mu}^2=p^2c^2+(mc^2)^2$
$E_{\nu}^2=p^2c^2$
$E_{\pi}^2 =~$

You understand that you need to use the equation $E^2=p^2c^2+(mc^2)^2$ for the square of the total energy and you are careful to use subscripts to denote which energy you are talking about but not careful enough. You also need to use subscripts on the right side of the equations. Note your use of the same symbol $p$ to denote the momentum of both the muon and the neutrino after the decay. Masses of particles also need subscripts wherever they appear.

You were unable to find an expression for $E_{\pi}^2$. Look at the general expression for the square of the total energy. How should it be rewritten if you have a pion at rest before it decays?

I got you started on the energy conservation equation. Similar steps need to be taken for the momentum conservation equation.

 

[PeroK]

... with these relativistic problems generally, if you are asked to find the KE, then the best approach is to find the total energy and then get the KE from that, by subtracting the rest energy. Introducing the KE into your equations too early just complicates things.

 

[jjson775]

The quadratic equation still has 2 unknowns. What is it that I am not seeing with this straightforward problem?

 

[PeroK]

View attachment 277526
The quadratic equation still has 2 unknowns. What is it that I am not seeing with this straightforward problem?

You're not using the other equations.

 

[kuruman]

Don't square both sides, at least not yet. Rewrite each term as I asked you. Leave unknowns alone - they will be sorted out after you write the momentum conservation equation.

 

[jtbell]

Perhaps you can use LaTeX which is easy to learn. Just click (tap) LaTeX Guide, lower left just above "Attach files" on this screen for a quick guide.

The guide says you can only display raw code using iOS.

That comment refers to the dedicated PF apps that were once available for iOS and Android. They were discontinued a few years ago IIRC, in favor of simply using a web browser.

LaTeX displays fine in Safari and Firefox on my iPad. Kuruman and PeroK are using LaTeX in their posts, and you can see those equations, right?

To see the raw LaTeX code, hit the "Reply" link on a post so you get the entire post quoted in the editing box.

On a desktop or notebook Mac, control-click on an equation to get a popup menu, then choose Show Math As --> TeX Commands. I haven't found a similar trick on an iPad.

By the way, momentum is the Latin letter $p$, not the Greek letter $\rho$ "rho".

 

[kuruman]

LaTeX displays fine in Safari and Firefox on my iPad. Kuruman and PeroK are using LaTeX in their posts, and you can see those equations, right?

LaTeX looks fine on my iPhone too with Safari and Firefox.

 

[jjson775]

That comment refers to the dedicated PF apps that were once available for iOS and Android. They were discontinued a few years ago IIRC, in favor of simply using a web browser.

LaTeX displays fine in Safari and Firefox on my iPad. Kuruman and PeroK are using LaTeX in their posts, and you can see those equations, right?

To see the raw LaTeX code, hit the "Reply" link on a post so you get the entire post quoted in the editing box.

On a desktop or notebook Mac, control-click on an equation to get a popup menu, then choose Show Math As --> TeX Commands. I haven't found a similar trick on an iPad.

By the way, momentum is the Latin letter $p$, not the Greek letter $\rho$ "rho".

Thanks, I will give LaTeX a shot. Also, I don’t know where I got the idea that momentum symbol is the Greek rho.

 

[jjson775]

Don't square both sides, at least not yet. Rewrite each term as I asked you. Leave unknowns alone - they will be sorted out after you write the momentum conservation equation.

I solved this problem although I had to go to the internet for another idea. The only trick was manipulating the algebra. Thanks for your suggestions.

 

[PeroK]

I solved this problem although I had to go to the internet for another idea. The only trick was manipulating the algebra. Thanks for your suggestions.

I still think you need to lose the habit of converting particle energies to joules, then back into $MeV$. The $eV$ is designed to be the appropriate unit for these problems, and particle masses are typically given in $MeV/c^2$.

Moreover, this is a standard problem of a mass $M$ decaying into a mass $m$ (particle 1) and a massless particle (2).

1) We have a common momentum $p$.

2) Conservation of energy gives $Mc^2 = E_1 + E_2$.

3) Using the E-M relation for each particle gives:

$E_1^2 - E_2^2 = p^2c^2 + m^2c^4 - p^2c^2 = m^2c^4$

4) $E_1^2 - E_2^2 = (E_1 - E_2)(E_1 + E_2) = (E_1 - E_2)Mc^2$

5) Equations 3) and 4) give:

$E_1 - E_2 = \frac{m^2c^2}{M}$

6) Combining equations 2) and 5) gives:

$E_1 = \frac{(M^2 + m^2)c^2}{2M}, \ \ E_2 = \frac{(M^2 - m^2)c^2}{2M}$

7) To get the kinetic energy we subtract the rest energy:

$K_1 = E_1 - mc^2 = \frac{(M-m)^2c^2}{2M}, \ \ K_2 = E_2$

8) In this case we have $M = 270m_e$, $m = 206 m_e$ and $m_e = 0.511MeV$, giving:

$K_1 = 7.58m_e c^2 = 3.88MeV$ and $K_2 = 56.4m_ec^2 = 28.8MeV$