- #1
bathtub2007
- 2
- 0
1. Problem Statement
Okay so I know these appear to be simple but for some reason I am having trouble finding the methods by which to solve them.
Problem 1:
This problem must be solved by reduction of order method and cannot use the y2 formula.
(1 - x^2)y'' + 2xy' = 0; y1 = 1
Problem 2:
This problem must be solved by reduction of order method and cannot use the y2 formula.
4x^2y'' + y = 0; y1 = [x^(1/2)]ln|x|
y2 / y1 = u (x)
y2 = u (x) * y1 (x)
y' = u'x + u
y'' = u''x +2u'
The general form for the problem is:
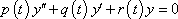
I have been trying to use Paul's Notes (http://tutorial.math.lamar.edu/Classes/DE/ReductionofOrder.aspx) to help me along the way but I am unable to follow for the lack of the teacher not exactly teaching the problems.
Any help getting towards the right direction would be much appreciated. Thank you.
Okay so I know these appear to be simple but for some reason I am having trouble finding the methods by which to solve them.
Problem 1:
This problem must be solved by reduction of order method and cannot use the y2 formula.
(1 - x^2)y'' + 2xy' = 0; y1 = 1
Problem 2:
This problem must be solved by reduction of order method and cannot use the y2 formula.
4x^2y'' + y = 0; y1 = [x^(1/2)]ln|x|
Homework Equations
y2 / y1 = u (x)
y2 = u (x) * y1 (x)
y' = u'x + u
y'' = u''x +2u'
The Attempt at a Solution
The general form for the problem is:
I have been trying to use Paul's Notes (http://tutorial.math.lamar.edu/Classes/DE/ReductionofOrder.aspx) to help me along the way but I am unable to follow for the lack of the teacher not exactly teaching the problems.
Any help getting towards the right direction would be much appreciated. Thank you.
Last edited by a moderator: