- #1
rollcast
- 408
- 0
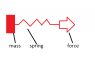
If you a mass being accelerated by a force which is acting upon a spring attached to the mass it will exhibit harmonic motion. However unlike a fixed harmonic oscillator there is no explicit solution to the equation which describes the motion of the mass in a reference frame outside of the system.
However what if you took the reference frame and imagined a reference frame where the mass or spring was stationary would this allow you to calculate an explicit solution for the equation?
Thanks
AL
However what if you took the reference frame and imagined a reference frame where the mass or spring was stationary would this allow you to calculate an explicit solution for the equation?
Thanks
AL