Reference Input for State Space Controller

[NeuralNet]

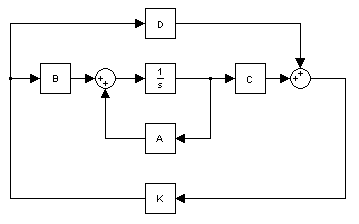
In the design of a State Space controller using state feedback the input to the plant is given as (where $y=x$ & $D=0$): $$u=-Kx$$

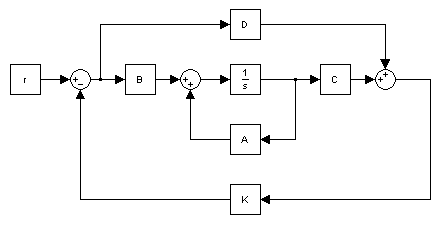
If there is a "reference input" then it would be:
$$u=-Kx+r$$

So the state feedback without the reference input simply drives all of the state variables to zero. When there is a reference input do the state variables get driven to match the values of the reference input?

 

[milesyoung]

Introducing a reference input in state-space design is a somewhat larger topic than in classic SISO theory. How you choose to include the reference input in the control topology can change the process dynamics considerably (especially when you include an estimator).

The question is very broad. Don't you have a good book on state-space design?

 

[NeuralNet]

Yes, but I can't find a good explanation of how the reference input works. I was trying to ask a very general question. Let me ask a very specific one instead.

My question is in regards to the section of "Adding precompensation" on this page:
http://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum&section=ControlStateSpace

I am confused about how after they add the precompensator they claim that "...the steady-state error of the cart's position has been eliminated". (I am referring to the third graph on the page).

If you look at the graph before that one the cart stabilizes at about -3mm (I think that means 3mm to the left). Then after they add the precompensator the cart stabilizes at 200mm (to the right?)!

How did that get rid of the steady state error? Is this a mistake?

 

[milesyoung]

Notice at the top where they list their design criteria, the objective is to adhere to some performance specifications for a 0.2 m step input. The third graph shows it settling to 0.2 m, as it should.

 

[NeuralNet]

But before they add that it only deviates 3mm from the initial point, which is much less than 200mm. Am I interpreting the graphs correctly: the cart moves to the left -3mm in the second graph, and to the right 200mm in the third graph?

 

[milesyoung]

You're missing the point. They _want_ it to go to 0.2 m, so the steady state error in the second graph is terrible (0.2 m - 0.003 m = a lot).

It's much better in the third graph as it settles to 0.2 m, i.e. there's no steady state error.

 

[NeuralNet]

Okay, so this brings me back to my original question. Is the goal of a reference input to drive the state to the point that matches the input?

 

[milesyoung]

Well, yes - the process state or output. The point of introducing the reference input is to have the process track it somehow. Did you have an other idea of what is what for?

 

[NeuralNet]

No, that is what I thought, but I wasn't sure. So for my application I am implementing the control system described on that page - but I want all of the states to go to zero, even after a step input (bumping the cart).

So do I just play around with that Nbar precompensator value until I get the steady state response of the cart to zero?

 

[milesyoung]

That whole 'adding precompensation' step is one of the control topologies you can use to introduce a reference input, but why do you want the system to be able to track a reference if you're not going to use it for anything? You could of course just do the design as they show and set r to the zero vector.

If you just want a regulator design that can reject disturbances, then you only need to do regular old full-state feedback with pole placement. I'd be very suprised if your book doesn't have a section/chapter on it.

 

[NeuralNet]

... why do you want the system to be able to track a reference if you're not going to use it for anything? You could of course just do the design as they show and set r to the zero vector.

If you just want a regulator design that can reject disturbances, then you only need to do regular old full-state feedback with pole placement.

That is what I thought, but my professor has argued with me about how I need a reference input. So I simply set the reference input to zero - i.e. just leave the reference input out?

So how would you suggest I account for a step input? Does the state feedback already account for that, or does it only account for the instabilities within the modeled plant?

 

[milesyoung]

... but I want all of the states to go to zero, even after a step input (bumping the cart).

I might have misunderstood what you meant here - I thought you meant a step input as in a disturbance which the regulator should reject.

Let me just get something straight then - do you want the system to be able to track a step input with zero steady state error? If so, then you need to use the design from the page you have linked or some other topology that includes a reference input.

 

[NeuralNet]

I want the system to stabilize the pendulum while keeping the cart toward the center of the track.

So it needs to balance the pendulum in its inverted state and if you tap the cart the pendulum needs to stay stabilized. That's it.

 

[milesyoung]

Then all you need is full-state feedback with pole placement.

So how would you suggest I account for a step input?

What do you mean by this though?

 

[NeuralNet]

When you bump the cart. That is what I am referring to as a step input.

Sorry for the confusion.

 

[milesyoung]

Alright, so no need for tracking. They use LQR design for pole placement in the page you have linked to - maybe you should stay clear of that for now to keep things simple.

The design procedure you need is straightforward and covered in any decent book on state-space design - usually in the first couple of chapters.

 

[NeuralNet]

So where in the block diagram does the step input actually occur if I don't want to track it?

 

[milesyoung]

At the reference input - I assume its 'r' in your second block diagram? Seems you just added it like you would with a classic SISO system.

Just use your first block diagram, you don't need the reference input. And again, I'd really recommend you have a readthrough of some basic state space design first.