You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Relating Path Difference and Intensity in Radar Signals
- Thread starter Saitama
- Start date
-
- Tags
- Radar Radio Radio waves Waves
AI Thread Summary
The discussion focuses on the relationship between path difference and intensity in radar signals, specifically addressing how to calculate path difference and its implications for constructive interference. Participants clarify that the path difference can be expressed as h/cos(α) and must equal nλ for constructive interference, where n is a positive integer. There is a debate about whether to include a phase shift due to reflection, which ultimately affects the calculations. The correct expression for minimum height h is derived as λ/(2cos(α)) when accounting for the phase shift. The conversation emphasizes the importance of accurately determining path difference to achieve the desired interference effects.
Physics news on Phys.org
rude man
Science Advisor
- 8,032
- 869
What is the phase difference requirement between two signals for totally constructive interference?
Saitama
- 4,244
- 93
Phase difference is equal to ##2n\pi## or path difference is ##n\lambda##.
rude man
Science Advisor
- 8,032
- 869
Pranav-Arora said:Phase difference is equal to ##2n\pi## or path difference is ##n\lambda##.
Correct. So you need n*lambda path difference. Solve for h?
Saitama
- 4,244
- 93
What is the value of n? 
I end up with ##h=n\lambda \cos \alpha##.
I end up with ##h=n\lambda \cos \alpha##.
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
n can be any positive integer. Are you sure that you got the correct expression for the path difference? Did you take into account the law of reflection? I wonder if you are meant to include a phase shift due to reflection?
rude man
Science Advisor
- 8,032
- 869
Pranav-Arora said:What is the value of n?
I end up with ##h=n\lambda \cos \alpha##.
Do you want to make the height higher than it has to be? You can make it ##h=\lambda \cos \alpha## or ##h=2\lambda \cos \alpha## or ...
I would make it as low as possible while satisfying your equation!
Saitama
- 4,244
- 93
TSny said:n can be any positive integer. Are you sure that you got the correct expression for the path difference? Did you take into account the law of reflection? I wonder if you are meant to include a phase shift due to reflection?
I don't know about considering the phase shift. There is nothing mentioned in the question about it. I think I got the right expression for path difference considering no phase shift. The given answer is ##\lambda/(4\cos \alpha)##.
rude man
Science Advisor
- 8,032
- 869
TSny said:n can be any positive integer. Are you sure that you got the correct expression for the path difference? Did you take into account the law of reflection? I wonder if you are meant to include a phase shift due to reflection?
Good point. I assumed the OP gave the correct path difference and I didn't consider any phase change due to reflection.
Judging from the given answer the path length was not what the OP came up with.
Saitama
- 4,244
- 93
rude man said:Good point. I assumed the OP gave the correct path difference and I didn't consider any phase change due to reflection.
Judging from the given answer the path length was not what the OP came up with.
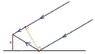
The light reflected from the surface of water which reaches the antenna has to travel an extra distance of ##h/\cos \alpha## (which can be easily calculated from simple trigonometry). This is the path difference. What have I done wrong?
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
Pranav-Arora said:The light reflected from the surface of water which reaches the antenna has to travel an extra distance of ##h/\cos \alpha## (which can be easily calculated from simple trigonometry). This is the path difference. What have I done wrong?
The two waves travel the same distance to the red dots shown in the figure.
Attachments
Saitama
- 4,244
- 93
Sorry for the late reply.
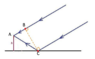
The length AC is ##h/\cos \alpha##.
##\angle ACB=2\alpha-\pi/2##
##\sin \angle ACB=AB/AC=AB\cos \alpha/h \Rightarrow -\cos 2\alpha=AB\cos \alpha/h##
##\Rightarrow AB=-h\cos 2\alpha/\cos \alpha##
Am I doing this right?
TSny said:The two waves travel the same distance to the red dots shown in the figure.
The length AC is ##h/\cos \alpha##.
##\angle ACB=2\alpha-\pi/2##
##\sin \angle ACB=AB/AC=AB\cos \alpha/h \Rightarrow -\cos 2\alpha=AB\cos \alpha/h##
##\Rightarrow AB=-h\cos 2\alpha/\cos \alpha##
Am I doing this right?
Attachments
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
Yes, that looks ok.
Saitama
- 4,244
- 93
TSny said:Yes, that looks ok.
Path difference is ##AC-AB=\frac{h}{\cos \alpha}+\frac{h\cos 2\alpha}{\cos \alpha}##
= \frac{h(1+\cos 2\alpha)}{\cos \alpha}=2h\cos \alpha
The path difference should be equal to ##n\lambda## and for min height, ##n=1##
\Rightarrow h=\frac{\lambda}{2\cos \alpha}
But this is wrong.
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
That all looks good. You might be expected to include a phase shift of the wave that reflects off the water.
Saitama
- 4,244
- 93
TSny said:That all looks good. You might be expected to include a phase shift of the wave that reflects off the water.
If I include the phase shift, I do get the right answer. Thank you TSny!
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
Good!
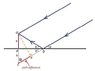
There's a trick that can make finding the path difference easier. In the figure, the tower is extended a distance h below the ground. You can use the law of reflection to show that the triangles abd and cbd are congruent. Then ba = bc and ec is the path difference.
There's a trick that can make finding the path difference easier. In the figure, the tower is extended a distance h below the ground. You can use the law of reflection to show that the triangles abd and cbd are congruent. Then ba = bc and ec is the path difference.
Attachments
Saitama
- 4,244
- 93
TSny said:There's a trick that can make finding the path difference easier. In the figure, the tower is extended a distance h below the ground. You can use the law of reflection to show that the triangles abd and cbd are congruent. Then ba = bc and ec is the path difference.
That makes it a lot easier, thanks!
Similar threads
- Replies
- 11
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 8
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 7
- Views
- 871
- Replies
- 3
- Views
- 1K
- Replies
- 2
- Views
- 2K
- Replies
- 4
- Views
- 664
- Replies
- 5
- Views
- 2K
Hot Threads
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 71
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math