- #1
analyst5
- 190
- 2
Hi guys, I was thinking about the relativistic effects a little bit, and I have a question regarding relative simultaneity.
Time dilation and length contraction grow as a function of the speed of the observer, and become noticeable and large on speeds close to the speed of light. By this sentence, I mean this, what's on the picture
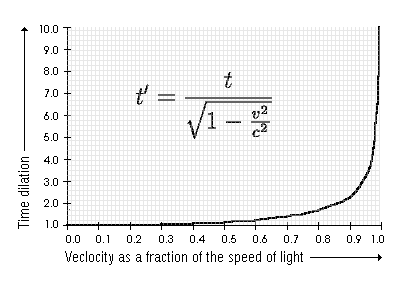
My question is: does relative simultaneity, or the time difference between two events progress by the same mathematical function, or is the time difference proportional to the velocity of the observer.
If it's not a problem, I would like to see a comparision between hyperplanes of simultaneity between different observers with different velocities so I can see how it differs between greater and slower speeds. I appreciate your help.
Time dilation and length contraction grow as a function of the speed of the observer, and become noticeable and large on speeds close to the speed of light. By this sentence, I mean this, what's on the picture
My question is: does relative simultaneity, or the time difference between two events progress by the same mathematical function, or is the time difference proportional to the velocity of the observer.
If it's not a problem, I would like to see a comparision between hyperplanes of simultaneity between different observers with different velocities so I can see how it differs between greater and slower speeds. I appreciate your help.