Relation between Sets AUFTRAG & KUNDE

[mathmari]

Hey! :giggle:

The below relations are given AUFTRAG($A_1, A_2, A_3$) and KUNDE($B_1, B_2, B_3$) with $A_1$ = AUFTRNR, $A_2$ = DATUM, $A_3$ = KUNDNR, $B_1$ = KUNDNR, $B_2$ = NAME and $B_3$ = ORT.

Determine the below sets or justify why it is not possible to determine them.

Let $A = A_1 \cup A_2 \cup A_3$ and $B = B_1 \cup B_2 \cup B_3$. Check if the below hold.

In a previous exercise I have shown the below relations (I suppose that they are useful here) :

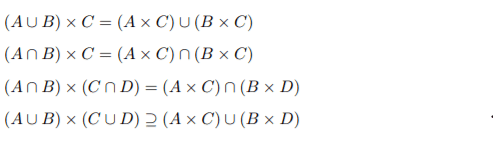I have done the following :

1. It holds that $\text{AUFTRAG}\cup \text{KUNDE} = (A_1, A_2, A_3)\cup (B_1, B_2, B_3)$. Since $A_3$ and $B_1$ are not entirely distinct we can use the first property, can't we? Or isn't this correct because these sets are notat the same position at the respective tupel? :unsure:

2. It holds that $\text{AUFTRAG}\cap \text{KUNDE} = (A_1, A_2, A_3)\cap (B_1, B_2, B_3)$. Here we can use the third property and so it holds that $\left (A_1\cap B_1 , A_2\cap B_2 , A_3\cap B_3\right )$, right? :unsure:

3. It holds that $\text{AUFTRAG}\times \text{KUNDE} = (A_1, A_2, A_3, B_1, B_2, B_3)$, or not? So we take all posible combinations for that set, don't we? :unsure:

4. We take the result of 3 and we replace $B_3$ everywhere by "Gießen", right? :unsure:

 

[I like Serena]

1. It holds that $\text{AUFTRAG}\cup \text{KUNDE} = (A_1, A_2, A_3)\cup (B_1, B_2, B_3)$. Since $A_3$ and $B_1$ are not entirely distinct we can use the first property, can't we? Or isn't this correct because these sets are not at the same position at the respective tupel?

Hey mathmari!

What do you mean by $(A_1, A_2, A_3)$ exactly?
I believe that e.g. $A_1$ is the set of all AUFTRAG numbers.
Strictly speaking $(A_1, A_2, A_3)$ would then be a tuple of 3 sets, which would be a single element of an unnamed set. (Worried)

Or did you mean $AUFTRAG=\text{AUFTRAG}(A_1,A_2,A_3)\subseteq A_1\times A_2\times A_3=\{(a_1,a_2,a_3)\mid a_1 \in A_1,a_2\in A_2, a_3\in A_3\}$?
Is $(A_1, A_2, A_3)$ perhaps a shorthand for the same thing? (Wondering)

Either way, I think we have:
\begin{align*}\text{AUFTRAG}\cup \text{KUNDE}
&=\{(124,\text{30.09.2020},7), \ldots, (667,\text{26.10.2021},13),(7,`\text{Schwarz'},`\text{Gieẞen'}),\ldots,(55,`\text{Roth'},`\text{Friedberg'})\} \\
&\subseteq A_1\times A_2\times A_3 \cup B_1\times B_2\times B_3 \\
&=\{(a_1,a_2,a_3)\mid a_1 \in A_1,a_2\in A_2, a_3\in A_3\}\cup\{(b_1,b_2,b_3)\mid b_1 \in B_1,b_2\in B_2, b_3\in B_3\}
\end{align*}
don't we? (Wondering)

These are incompatible tupels, but that is okay for a set. We just have a set of different types.

2. It holds that $\text{AUFTRAG}\cap \text{KUNDE} = (A_1, A_2, A_3)\cap (B_1, B_2, B_3)$. Here we can use the third property and so it holds that $\left (A_1\cap B_1 , A_2\cap B_2 , A_3\cap B_3\right )$, right?

Each tupel in AUFTRAG is a single element. None of these tupels occur in KUNDE, do they?

3. It holds that $\text{AUFTRAG}\times \text{KUNDE} = (A_1, A_2, A_3, B_1, B_2, B_3)$, or not? So we take all posible combinations for that set, don't we?

I believe we need to match each row in AUFTRAG with each row in KUNDE and write them as 6-tupels.

4. We take the result of 3 and we replace $B_3$ everywhere by "Gießen", right?

I believe we are supposed to take the subset of the result of 3 of the tupels that have "Gießen" in them.
The symbol $\sigma_{condition}$ means SELECT WHERE condition.

 

[mathmari]

What do you mean by $(A_1, A_2, A_3)$ exactly?
I believe that e.g. $A_1$ is the set of all AUFTRAG numbers.
Strictly speaking $(A_1, A_2, A_3)$ would then be a tuple of 3 sets, which would be a single element of an unnamed set. (Worried)

Or did you mean $AUFTRAG=\text{AUFTRAG}(A_1,A_2,A_3)\subseteq A_1\times A_2\times A_3=\{(a_1,a_2,a_3)\mid a_1 \in A_1,a_2\in A_2, a_3\in A_3\}$?

We have that AUFTRAG and KUNDE are relations.

For the union of the relations $R$ ans $S$ with $R(A_1, \ldots , A_n)$ and $S(B_1, \ldots , B_m)$ we have $$R\cup S=R'(A_1, \ldots , A_n)$$ that is produced by $$R'=\{t\mid t\in R\lor t\in S\}$$

For the cartesian product we have $$R\times S=R'(A_1, \ldots , A_n, B_1, \ldots , B_m)$$ that is produced by $$R'=\{r\cdot s\mid r\in R\land s\in nS\}$$ where $r\cdot s=(r_1, \ldots , r_n, s_1, \ldots , s_m)$ when $r=(r_1, \ldots , r_n)\in R$ and $s=(s_1, \ldots , s_n)\in S$.

Either way, I think we have:
\begin{align*}\text{AUFTRAG}\cup \text{KUNDE}
&=\{(124,\text{30.09.2020},7), \ldots, (667,\text{26.10.2021},13),(7,`\text{Schwarz'},`\text{Gieẞen'}),\ldots,(55,`\text{Roth'},`\text{Friedberg'})\} \\
&\subseteq A_1\times A_2\times A_3 \cup B_1\times B_2\times B_3 \\
&=\{(a_1,a_2,a_3)\mid a_1 \in A_1,a_2\in A_2, a_3\in A_3\}\cup\{(b_1,b_2,b_3)\mid b_1 \in B_1,b_2\in B_2, b_3\in B_3\}
\end{align*}
don't we? (Wondering)

These are incompatible tupels, but that is okay for a set. We just have a set of different types.

From the above definition of the union we get that $$
\text{AUFTRAG}\cup \text{KUNDE}=\{(124,\text{30.09.2020},7), \ldots, (667,\text{26.10.2021},13),(7,`\text{Schwarz'},`\text{Gieẞen'}),\ldots,(55,`\text{Roth'},`\text{Friedberg'})\}$$ as you wrote, right? :unsure:

Do you mean that these are incompatible tupels because they are different "things", for example at the last ones the last component is a city but at the first elements the last component is a number? Or did you mean something else? :unsure:

Each tupel in AUFTRAG is a single element. None of these tupels occur in KUNDE, do they?

The intersection would mean that each component of a tupel must be the same in AUFTRAG and in KUNDE, right? :unsure:

I believe we need to match each row in AUFTRAG with each row in KUNDE and write them as 6-tupels.

So that means that we get $$\{(124, \ 30.09.2021, \ 7, \ 7, \ \text{Schwarz} \ , \ \text{Gießen}), (124, \ 30.09.2021, \ 7, \ 13, \ \text{Weiss} \ , \ \text{Wetzlar}), \ldots \}$$ right? :unsure:

I believe we are supposed to take the subset of the result of 3 of the tupels that have "Gießen" in them.
The symbol $\sigma_{condition}$ means SELECT WHERE condition.

So we take the elements of $\text{AUFTRAG}\times \text{KUNDE}$ that has the element "Gießen" as the last component, right? :unsure:

 

[I like Serena]

We have that AUFTRAG and KUNDE are relations.

For the union of the relations $R$ ans $S$ with $R(A_1, \ldots , A_n)$ and $S(B_1, \ldots , B_m)$ we have $$R\cup S=R'(A_1, \ldots , A_n)$$ that is produced by $$R'=\{t\mid t\in R\lor t\in S\}$$

For the cartesian product we have $$R\times S=R'(A_1, \ldots , A_n, B_1, \ldots , B_m)$$ that is produced by $$R'=\{r\cdot s\mid r\in R\land s\in nS\}$$ where $r\cdot s=(r_1, \ldots , r_n, s_1, \ldots , s_m)$ when $r=(r_1, \ldots , r_n)\in R$ and $s=(s_1, \ldots , s_n)\in S$.

Good. (Nod)

But what is $(A_1, \ldots , A_n)$?

Note that $R(A_1, \ldots , A_n)$ means that we have a relationship $R$ that is a function of the sets $A_1$ up to $A_n$, which is different from a tupel of sets.

From the above definition of the union we get that $$
\text{AUFTRAG}\cup \text{KUNDE}=\{(124,\text{30.09.2020},7), \ldots, (667,\text{26.10.2021},13),(7,`\text{Schwarz'},`\text{Gieẞen'}),\ldots,(55,`\text{Roth'},`\text{Friedberg'})\}$$ as you wrote, right?

Yes. (Nod)

Do you mean that these are incompatible tupels because they are different "things", for example at the last ones the last component is a city but at the first elements the last component is a number? Or did you mean something else?

Indeed.
In this particular case both types of elements are 3-tupels, but that is not necessarily the case.
We could also have 4-tupels in the same set from yet another table.

The intersection would mean that each component of a tupel must be the same in AUFTRAG and in KUNDE, right?

Yep.

So that means that we get $$\{(124, \ 30.09.2021, \ 7, \ 7, \ \text{Schwarz} \ , \ \text{Gießen}), (124, \ 30.09.2021, \ 7, \ 13, \ \text{Weiss} \ , \ \text{Wetzlar}), \ldots \}$$ right?

Correct. (Nod)

So we take the elements of $\text{AUFTRAG}\times \text{KUNDE}$ that has the element "Gießen" as the last component, right?

Yep.

 

[mathmari]

But what is $(A_1, \ldots , A_n)$?

Note that $R(A_1, \ldots , A_n)$ means that we have a relationship $R$ that is a function of the sets $A_1$ up to $A_n$, which is different from a tupel of sets.

The $(A_1, \ldots , A_n)$ from $R$ is different from $R'$, right? :unsure:

 

[I like Serena]

The $(A_1, \ldots , A_n)$ from $R$ is different from $R'$, right?

There are two references to $R'$ in what you wrote that are different.
The second $R'$ is a function of $(A_1, \ldots , A_n,B_1,\ldots, B_m)$.
It seems to me that the first one should also be a function of $(A_1, \ldots , A_n,B_1,\ldots, B_m)$. (Tauri)

If that is the case then the $(A_1, \ldots , A_n)$ from $R$ are the same as the ones from $R'$ as they should.

 

[mathmari]

At 7 the left side is the elements of AUFTRAG that have the as KUNDNR numbers that occur also in KUNDE right?
At 7 the right side is the first three columns of the result of the parenthesis, right?

At 9 the left side is a kind of concatenation of the elements of AUFTRAG that have the as KUNDNR numbers that occur also in KUNDE right?

:unsure:

 

[I like Serena]

At 7 the left side is the elements of AUFTRAG that have the as KUNDNR numbers that occur also in KUNDE right?
At 7 the right side is the first three columns of the result of the parenthesis, right?

At 9 the left side is a kind of concatenation of the elements of AUFTRAG that have the as KUNDNR numbers that occur also in KUNDE right?

Yes to everything. (Nod)

They are called a left semijoin ($\ltimes$), projection ($\pi_{a_1\ldots a_n}$), respectively natural join ($\Join$). (Nerd)

 

[mathmari]

So do we have the following ? Question 1 :

Question 2 :

Question 3 :

Question 4 :

Question 5 :

Therefore

Question 6 :

So it is the same as KUNDE.

Question 7 :

So we see that the equality holds.
Question 8 :
We have that $A\cap B=\text{KUNDNR}$. So we get :

So we see that the equality holds. Question 9 :

So we see that the equality holds.
Question 10 :

So we see that the equality holds.

Is everything correct and complete? :unsure:

 

[mathmari]

I read now in the notes :
The prerequisite for the union of $R$ and $S$ is their compatibility, i.e., Rank (R) = Rank (S) and for all $i = 1, 2,\ldots , n$ it should hold that dom($A_i$) = dom($B_i$).

What exactly does that mean? Are these conditions satisfied in this case? :unsure:

 

[I like Serena]

I read now in the notes :
The prerequisite for the union of $R$ and $S$ is their compatibility, i.e., Rank (R) = Rank (S) and for all $i = 1, 2,\ldots , n$ it should hold that dom($A_i$) = dom($B_i$).

What exactly does that mean? Are these conditions satisfied in this case?

It means that R and S must have exactly the same column headers.

So do we have the following ?

Question 1 :
View attachment 11397

So question 1 is not correct after all. Instead we can't take the union.

Question 2 :

Question 3 :

Question 4 :

All correct. (Nod)

Question 5 :
View attachment 11401

This does not look correct. The data in the rows does not match the column headers.
The column headers should be first the ones from KUNDE and then from AUFTRAG. (Worried)

Therefore
View attachment 11402

Perhaps there is a note about this?
It may have been intended that if the columns are ordered differently, that the rows still match.

Question 6 :
https://www.physicsforums.com/attachments/11403

So it is the same as KUNDE.

I think so yes. (Nod)

Question 7 :
So we see that the equality holds.

Question 8 :
We have that $A\cap B=\text{KUNDNR}$. So we get :
So we see that the equality holds.

Question 9 :
So we see that the equality holds.

Question 10 :
So we see that the equality holds.

Yep. (Nod)

 

[mathmari]

It means that R and S must have exactly the same column headers.

So question 1 is not correct after all. Instead we can't take the union.

Ah so the two sets have to have exactly the same titels of columns, right? :unsure:

This does not look correct. The data in the rows does not match the column headers.
The column headers should be first the ones from KUNDE and then from AUFTRAG. (Worried)

Perhaps there is a note about this?
It may have been intended that if the columns are ordered differently, that the rows still match.

Ah I didn't change the titels of the columns... So do we have the following :

About the intersection we have $R\cap S=R\setminus (R\setminus S)$. That means that (AUFTRAG $\times$ KUNDE) $\cap$ (KUNDE $\times$ AUFTRAG) is the table of (AUFTRAG $\times$ KUNDE) without the columns of (KUNDE $\times$ AUFTRAG) and then we consider the table of (AUFTRAG $\times$ KUNDE) without the columns of the previous result, right? :unsure:

 

[I like Serena]

Ah so the two sets have to have exactly the same titels of columns, right?

Yes. (Nod)

Ah I didn't change the titels of the columns... So do we have the following :

Yep. (Nod)

About the intersection we have $R\cap S=R\setminus (R\setminus S)$. That means that (AUFTRAG $\times$ KUNDE) $\cap$ (KUNDE $\times$ AUFTRAG) is the table of (AUFTRAG $\times$ KUNDE) without the columns of (KUNDE $\times$ AUFTRAG) and then we consider the table of (AUFTRAG $\times$ KUNDE) without the columns of the previous result, right?

If I'm not mistaken the intersection consists of the columns and rows that $R$ and $S$ have in common.
It means that we answered question 2 incorrectly.
Question 2 should have only 1 column for KUNDE, and it should have 3 rows for the ones that AUFTRAG and KUNDE have in common.

For question 5, we have that AUFTRAG $\times$ KUNDE and KUNDE $\times$ AUFTRAG have the same columns although in a different order, and they also have the same rows.
The corresponding $R\setminus S$ has no columns nor rows at all. It is the empty set. When we subtract that again from $R$ we simply have $R$.
So I believe that (AUFTRAG $\times$ KUNDE) $\cap$ (KUNDE $\times$ AUFTRAG) = AUFTRAG $\times$ KUNDE.

 

[mathmari]

If I'm not mistaken the intersection consists of the columns and rows that $R$ and $S$ have in common.
It means that we answered question 2 incorrectly.
Question 2 should have only 1 column for KUNDE, and it should have 3 rows for the ones that AUFTRAG and KUNDE have in common.

I havn't really understood that part.

First we consider $R\setminus S$, so at the table AUFTRAG we delete the elements that are also in KUNDE.
The column KUNDNR is common so we delete the rows that are in common.

We delete this row from AUFTRAG and get :

Is that correct? :unsure:

 

[I like Serena]

First we consider $R\setminus S$, so at the table AUFTRAG we delete the elements that are also in KUNDE.
The column KUNDNR is common so we delete the rows that are in common.

We delete this row from AUFTRAG and get :

I believe we should also delete the columns that are in common.
So
$$AUFTRAG\setminus KUNDE=\begin{array}{|c|c|}\hline
AUFTRNR & DATUM\\
\hline
378 & 17.10.2021 \\
\hline
\end{array}$$

Delete those columns and that row from AUFTRAG, and keep only the unique rows to get:
$$AUFTRAG\cap KUNDE = AUFTRAG\setminus(AUFTRAG\setminus KUNDE)=\begin{array}{|c|}\hline
KUNDNR\\
\hline
7 \\
\hline
27\\
\hline
13 \\
\hline
\end{array}$$

 

[mathmari]

I believe we should also delete the columns that are in common.
So
$$AUFTRAG\setminus KUNDE=\begin{array}{|c|c|}\hline
AUFTRNR & DATUM\\
\hline
378 & 17.10.2021 \\
\hline
\end{array}$$

Delete those columns and that row from AUFTRAG, and keep only the unique rows to get:
$$AUFTRAG\cap KUNDE = AUFTRAG\setminus(AUFTRAG\setminus KUNDE)=\begin{array}{|c|}\hline
KUNDNR\\
\hline
7 \\
\hline
27\\
\hline
13 \\
\hline
\end{array}$$

Ah ok! I see! Thank you! (Flower)

 

[mathmari]

We consider the relations AUFTRAG and KUNDE and create an expression for each of the below from the algebra of relations.

1. Create an expression that lists all possible combinations of customer numbers (KUNDNR) and locations (ORT).
2. Create an expression that lists all customer names (NAME) with at least one order (Auftrag).
3. Create an expression that lists all order numbers (AUFTRAGNR) with customers from Gießen or Wetzlar.
4. Create an expression that lists all customer numbers (KUNDNR) without an order (Auftrag).
5. Create an expression that lists all customer numbers (KUNDNR) that are not assigned to any order (Auftrag) and all customer numbers (KUNDNR) to which no name (NAME) is assigned.Do we have the following ?

1. $\pi_{\text{KUNDNR}, \text{ORT}}(\text{AUFTRAG}\times\text{KUNDE})$
2. So we want all NAMES where the corresponding KUNDNR is also in AUFTRAG, right?
3. $\pi_{AUFTRAGNR}\left (\sigma_{B_3='\text{Gießen}, B_3='\text{Wetzlar}'}(\text{AUFTRAG}\times\text{KUNDE})\right )$
4. Do we use Division here?
5. Do weuse again Division?

:unsure:

 

[I like Serena]

1. $\pi_{\text{KUNDNR}, \text{ORT}}(\text{AUFTRAG}\times\text{KUNDE})$

That works.
We don't need AUFTRAG at all though. I believe we can simplify it to $\pi_{\text{KUNDNR}, \text{ORT}}(\text{KUNDE})$.

2. So we want all NAMES where the corresponding KUNDNR is also in AUFTRAG, right?

Yep.
We can use a semijoin or the natural join to find them.

3. $\pi_{AUFTRAGNR}\left (\sigma_{B_3='\text{Gießen}, B_3='\text{Wetzlar}'}(\text{AUFTRAG}\times\text{KUNDE})\right )$

That won't work. (Shake)

Note that $\text{AUFTRAG}\times\text{KUNDE}$ consists of the combination of every possible row in AUFTRAG with every possible row in KUNDE - even if they don't match. (Worried)
Moreover, I think $\sigma_{B_3=`\text{Gießen'}, B_3=`\text{Wetzlar'}}$ means to select on $B_3=`\text{Gießen'} \operatorname{AND} B_3=`\text{Wetzlar'}$, which will then result in an empty set as they are mutually exclusive. (Worried).

4. Do we use Division here?
5. Do we use again Division?

Division means that we consider some rows equivalent and merge them together, eliminating the distinction on a field that they otherwise have.
I don't see how we can use that here. :unsure:

Perhaps we can use set difference instead.

 

[mathmari]

That works.
We don't need AUFTRAG at all though. I believe we can simplify it to $\pi_{\text{KUNDNR}, \text{ORT}}(\text{KUNDE})$.

Ah yes!

Note that $\text{AUFTRAG}\times\text{KUNDE}$ consists of the combination of every possible row in AUFTRAG with every possible row in KUNDE - even if they don't match. (Worried)
Moreover, I think $\sigma_{B_3=`\text{Gießen'}, B_3=`\text{Wetzlar'}}$ means to select on $B_3=`\text{Gießen'} \operatorname{AND} B_3=`\text{Wetzlar'}$, which will then result in an empty set as they are mutually exclusive. (Worried).

So we have to write these as two different $\sigma$'s then? :unsure:

Division means that we consider some rows equivalent and merge them together, eliminating the distinction on a field that they otherwise have.
I don't see how we can use that here. :unsure:

Perhaps we can use set difference instead.

At 4. do we have the set difference of KUNDE and AUFTRAG and then from the result we take the projection of KUNDNR? :unsure:

 

[I like Serena]

So we have to write these as two different $\sigma$'s then?

According to wiki, we can do it in a single $\sigma$, but we should use $\lor$ instead of '$,$', since the latter usually means $\land$.

At 4. do we have the set difference of KUNDE and AUFTRAG and then from the result we take the projection of KUNDNR?

I think that the column KUNDNR is deleted completely if the take the set difference $KUNDE \setminus AUFTRAG$.
Then we don't have what we need anymore. (Worried)

 

[mathmari]

I think that the column KUNDNR is deleted completely if the take the set difference $KUNDE \setminus AUFTRAG$.
Then we don't have what we need anymore. (Worried)

Do we maybe do at 4 : $KUNDE \setminus (AUFTRAG \cap KUNDE )$ ? :unsure:

 

[I like Serena]

4. Create an expression that lists all customer numbers (KUNDNR) without an order (Auftrag).

Do we maybe do at 4 : $KUNDE \setminus (AUFTRAG \cap KUNDE )$ ? :unsure:

To be honest, I'm at a loss what set difference even means in this context.
Does it delete columns that we have in common or not?
Do you perchance have a quote?

Either way, I think $AUFTRAG \cap KUNDE$ gives us the list of KUNDNR that does have a match.
So we need to remove those from the list of all KUNDNR's that we have in KUNDE.
I think that should be $\pi_{KUNDNR}(KUNDE)\setminus \pi_{KUNDNR}(AUFTRAG \cap KUNDE)$. :unsure:

 

[mathmari]

To be honest, I'm at a loss what set difference even means in this context.
Does it delete columns that we have in common or not?
Do you perchance have a quote?

The difference $R \setminus S$ deletes the tuples from the first relation that occurs also in the second relation.

An example :

Either way, I think $AUFTRAG \cap KUNDE$ gives us the list of KUNDNR that does have a match.
So we need to remove those from the list of all KUNDNR's that we have in KUNDE.
I think that should be $\pi_{KUNDNR}(KUNDE)\setminus \pi_{KUNDNR}(AUFTRAG \cap KUNDE)$. :unsure:

Ahh ok!

Isn't $\pi_{KUNDNR}(AUFTRAG \cap KUNDE)=AUFTRAG \cap KUNDE$, since at the intersection wehad only the column KUNDNR ? :unsure:

At 5 do we take the column KUNDNR of KUNDE and we compare this if it occurs in AUFTRAG and we take only these that are not occurred there and then we take the KUNDNR of AUFTRAG and wecompare thisif it occurs in KUNDE and we take only these that are not occurred there ? :unsure:

 

[I like Serena]

The difference $R \setminus S$ deletes the tuples from the first relation that occurs also in the second relation.

An example :

That seems to imply that we require that both relations have the same columns, or it won't be defined.
Is that the case? :unsure:

Isn't $\pi_{KUNDNR}(AUFTRAG \cap KUNDE)=AUFTRAG \cap KUNDE$, since at the intersection we had only the column KUNDNR ?

I guess so. I was just being extra careful since I wasn't entirely sure what intersection and set difference meant in this context. :unsure:

5. Create an expression that lists all customer numbers (KUNDNR) that are not assigned to any order (Auftrag) and all customer numbers (KUNDNR) to which no name (NAME) is assigned.

At 5 do we take the column KUNDNR of KUNDE and we compare this if it occurs in AUFTRAG and we take only these that are not occurred there and then we take the KUNDNR of AUFTRAG and wecompare this if it occurs in KUNDE and we take only these that are not occurred there ?

Sounds about right. It also sounds as if we need to take the union of two expressions. :unsure:

 

[mathmari]

When I see the below :

at the difference I suppose that all columns that are in R shouldalso be in S and since the intersection is defined as $R\cap S=R\setminus (R\setminus S)$ then $R$ and $S$ should again be compatible, or not? :unsure:

So at union, difference and intersection we should have the same number of columns and the same columns, or have I understood that wrong? :unsure:

 

[I like Serena]

When I see the below :

at the difference I suppose that all columns that are in R should also be in S and since the intersection is defined as $R\cap S=R\setminus (R\setminus S)$ then $R$ and $S$ should again be compatible, or not? :unsure:

So at union, difference and intersection we should have the same number of columns and the same columns, or have I understood that wrong? :unsure:

In that screenshot we see that union and set difference have been defined for R and S that have exactly the same columns.
It seems to imply that union and set difference are not defined if the columns are not exactly the same.

If intersection has been defined as $R\cap S=R\setminus (R\setminus S)$, then the same thing applies.
If the columns are not exactly the same, then the intersection is not defined.

 

[mathmari]

In that screenshot we see that union and set difference have been defined for R and S that have exactly the same columns.
It seems to imply that union and set difference are not defined if the columns are not exactly the same.

If intersection has been defined as $R\cap S=R\setminus (R\setminus S)$, then the same thing applies.
If the columns are not exactly the same, then the intersection is not defined.

Ok! So at union, intersection and difference the relations must be compatible. So do we have the following ?

1. $\pi_{\text{KUNDNR}, \text{ORT}}(\text{KUNDE})$

2. $\text{KUNDE} \ltimes \text{AUFTRAG}$

3. $\pi_{\text{AUFTRAGNR}}\left (\sigma_{B_3='\text{Gießen}\lor B_3='\text{Wetzlar}'}(\text{AUFTRAG}\times\text{KUNDE})\right )$

4. $\pi_{\text{KUNDNR}}(\text{KUNDE}) \setminus \pi_{\text{KUNDNR}}(\text{AUFTRAG})$

5. $\left [\pi_{\text{KUNDNR}}(\text{KUNDE}) \setminus \pi_{\text{KUNDNR}}(\text{AUFTRAG}) \right ]\cup \left [\pi_{\text{KUNDNR}}(\text{AUFTRAG}) \setminus \pi_{\text{KUNDNR}}(\text{KUNDE})\right ]$

:unsure:

 

[I like Serena]

We consider the relations AUFTRAG and KUNDE and create an expression for each of the below from the algebra of relations.

1. Create an expression that lists all possible combinations of customer numbers (KUNDNR) and locations (ORT).
2. Create an expression that lists all customer names (NAME) with at least one order (Auftrag).
3. Create an expression that lists all order numbers (AUFTRAGNR) with customers from Gießen or Wetzlar.
4. Create an expression that lists all customer numbers (KUNDNR) without an order (Auftrag).
5. Create an expression that lists all customer numbers (KUNDNR) that are not assigned to any order (Auftrag) and all customer numbers (KUNDNR) to which no name (NAME) is assigned.

1. $\pi_{\text{KUNDNR}, \text{ORT}}(\text{KUNDE})$

Yes. (Nod)

2. $\text{KUNDE} \ltimes \text{AUFTRAG}$

No. (Shake)

3. $\pi_{\text{AUFTRAGNR}}\left (\sigma_{B_3='\text{Gießen}\lor B_3='\text{Wetzlar}'}(\text{AUFTRAG}\times\text{KUNDE})\right )$

Yes. (Nod)

4. $\pi_{\text{KUNDNR}}(\text{KUNDE}) \setminus \pi_{\text{KUNDNR}}(\text{AUFTRAG})$

Yes. (Nod)

5. $\left [\pi_{\text{KUNDNR}}(\text{KUNDE}) \setminus \pi_{\text{KUNDNR}}(\text{AUFTRAG}) \right ]\cup \left [\pi_{\text{KUNDNR}}(\text{AUFTRAG}) \setminus \pi_{\text{KUNDNR}}(\text{KUNDE})\right ]$

Yes. (Nod)

 

[mathmari]

No. (Shake)

Ah do we have to take also the projection of the result? I mean $\pi_{\text{NAME}}(\text{KUNDE} \ltimes \text{AUFTRAG})$ :unsure:

 

[I like Serena]

Ah do we have to take also the projection of the result? I mean $\pi_{\text{NAME}}(\text{KUNDE} \ltimes \text{AUFTRAG})$

Yep.
The questions only asks for the NAME's, so we should have an expression that returns only those.

 

[mathmari]

Create an expression for the below in the domain relational calculus and and an expression in the tuple calculus.

1. Create an expression that lists all possible combinations of customer numbers (KUNDNR) and locations (ORT).
2. Create an expression that lists all customer names (NAME) with at least one order (Auftrag).
3. Create an expression that lists all order numbers (AUFTRAGNR) with customers from Gießen or Wetzlar.
4. Create an expression that lists all customer numbers (KUNDNR) without an order (Auftrag).
5. Create an expression that lists all customer numbers (KUNDNR) that are not assigned to any order (Auftrag) and all customer numbers (KUNDNR) to which no name (NAME) is assigned.
Let's start with the first two (Malthe)

1 : We have written this with the expression $\pi_{\text{KUNDNR}, \text{ORT}}(\text{KUNDE})$ which can be written in relational calculus with the expression $\{y_1, y_2\mid \exists x_1, x_2, x_3\left (\text{KUNDE}(x_1, x_2, x_3)\land y_1=x_1\land y_2=x_3\right \}$, right? :unsure:

2 : We have written this with the expression $\pi_{\text{NAME}}(\text{KUNDE} \ltimes \text{AUFTRAG})$ which can be written in relational calculus with the expression $\{y \mid \exists x_1, x_2, x_3\left (\text{KUNDE} \ltimes \text{AUFTRAG}(x_1, x_2, x_3)\land y_1=x_1\land y_2=x_3\right \}$, right? Now we have to write also the left join in relational calculus, or not? :unsure:

 

[I like Serena]

Looks about right to me. (Nod)

 

[I like Serena]

1 : We have written this with the expression $\pi_{\text{KUNDNR}, \text{ORT}}(\text{KUNDE})$ which can be written in relational calculus with the expression $\{y_1, y_2\mid \exists x_1, x_2, x_3\left (\text{KUNDE}(x_1, x_2, x_3)\land y_1=x_1\land y_2=x_3\right \}$, right?

Btw, we can also write $\{(kundnr, ort)\mid \exists name\left (\text{KUNDE}(kundnr, name, ort)\right \}$ can't we?

 

[mathmari]

Btw, we can also write $\{(kundnr, ort)\mid \exists name\left (\text{KUNDE}(kundnr, name, ort)\right \}$ can't we?

Ah ok!

How does an expression in the tuple calculus look like? What is the edifference to the above ? Is the first part of the maybe a tuple ? I mean, is maybe the expression you wrote in #33 in tuple calculus? :unsure:

 

[mathmari]

As for the tuple calculus I found ine the notes the below example :

So at 1 we have then $$\{(k.KUNDNR, k.ORT)\mid \left (\text{KUNDE}(k)\right \}$$ or not? :unsure: