hicetnunc
- 13
- 5
- Homework Statement
- An emission line in the spectrum of an alkali has three fine-structure components corresponding to the transitions ##^2\text{P}_{3/2} - ^2\text{D}_{3/2}##, ##^2\text{P}_{3/2} - ^2\text{D}_{5/2}## and ##^2\text{P}_{1/2} - ^2\text{D}_{3/2}##. These components have intensities ##a##, ##b## and ##c##, respectively, that are in the ratio ##1:9:5##. Show that these satisfy the rule that the sum of the intensities of the transitions to, or from, a given level is proportional to its statistical weight (##2J+1##).
- Relevant Equations
- None.
Hi. I'm really stuck with this problem and would appreciate some help.
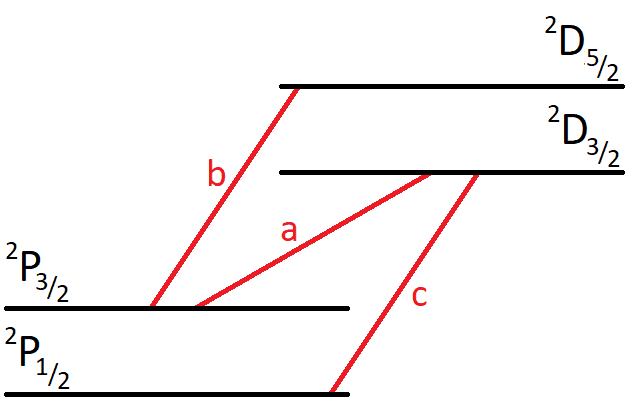
For example, if i take the total intensity from the ##^2\text{P}_{3/2}## level, i get ##a+b##. Since ##b## is 9 times larger than ##a##, i get that the total intensity is ##10a##. This should then be proportional to the statistical weight ##2J+1=4##, so ##10a = 4q##, where ##q## is a proportionality constant. Then ##q=2.5a##. But if I then consider the ##^2\text{D}_{3/2}## level, I get that its total intensity is ##a+c=6a## and has statistical weight 4. Then the proportionality constant would be ##q=\frac{6a}{4}=1.5a##. This doesn't seem right since I get different proportionality constants.
How should I handle this problem?
For example, if i take the total intensity from the ##^2\text{P}_{3/2}## level, i get ##a+b##. Since ##b## is 9 times larger than ##a##, i get that the total intensity is ##10a##. This should then be proportional to the statistical weight ##2J+1=4##, so ##10a = 4q##, where ##q## is a proportionality constant. Then ##q=2.5a##. But if I then consider the ##^2\text{D}_{3/2}## level, I get that its total intensity is ##a+c=6a## and has statistical weight 4. Then the proportionality constant would be ##q=\frac{6a}{4}=1.5a##. This doesn't seem right since I get different proportionality constants.
How should I handle this problem?