Jtappan
- 95
- 0
Homework Statement
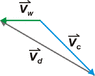
A dolphin wants to swim directly back to its home bay, which is 0.79 km due west. It can swim at a speed of 4.14 m/s relative to the water, but a uniform water current flows with speed 2.93 m/s in the southeast direction.
(a) What direction should the dolphin head?
_______° N of W
(b) How long does it take the dolphin to swim the 0.79-km distance home?
________min
Homework Equations
kinematics equations