fulis
- 6
- 0
Hi,
I was looking up the formula for this on wikipedia and it said that the frequency shift is:
\frac{\sqrt{1 - v^2/c^2}}{1+\frac{v}{c}\cos{\theta}}
In the case where the the emitter is directly above the observer when the photon arrives it says it simplifies to:
\gamma = \frac{1}{\sqrt{1 - v^2/c^2}}
Now, I can't get that to work out.
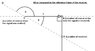
In this special case we have that:
\cos{\theta}=\frac{v}{c}
So the doppler shift becomes:
\frac{\sqrt{1 - v^2/c^2}}{1+v^2/c^2}
which doesn't cancel the numerator because there's a minus sign missing.
If you take the same situation but reverse the direction of v nothing changes because the new angle becomes \pi-\theta, so the sign of the cosine term cancels the minus sign from v, which is clearly wrong since it should go from a blueshift to a redshift. Is there supposed to be a +/- in front of the cosine term?
I was looking up the formula for this on wikipedia and it said that the frequency shift is:
\frac{\sqrt{1 - v^2/c^2}}{1+\frac{v}{c}\cos{\theta}}
In the case where the the emitter is directly above the observer when the photon arrives it says it simplifies to:
\gamma = \frac{1}{\sqrt{1 - v^2/c^2}}
Now, I can't get that to work out.
In this special case we have that:
\cos{\theta}=\frac{v}{c}
So the doppler shift becomes:
\frac{\sqrt{1 - v^2/c^2}}{1+v^2/c^2}
which doesn't cancel the numerator because there's a minus sign missing.
If you take the same situation but reverse the direction of v nothing changes because the new angle becomes \pi-\theta, so the sign of the cosine term cancels the minus sign from v, which is clearly wrong since it should go from a blueshift to a redshift. Is there supposed to be a +/- in front of the cosine term?
 But you're still apparently missing something: the Wikipedia page talks about *two* cases, not just one.
But you're still apparently missing something: the Wikipedia page talks about *two* cases, not just one.