I Relativity paradox: rocket landing in a cylinder

[wnvl2]

TL;DR

Relativity paradox about a rocket landing in a cylinder. Rocket and cylinder both have the same length L.

A rocket has length L with a separate head on top. The rocket lands in a cilinder on Earth with height L with speed v. From the point of view of the rocket, the cylinder undergoes a Lorentz contraction. The rocket will therefore collide with the bottom of the cilinder and damage it. From the perspective of the tube, the rocket will undergo a Lorentz contraction. The result is that the head of the rocket will collide with the top of the cylinder and the head will be damaged.

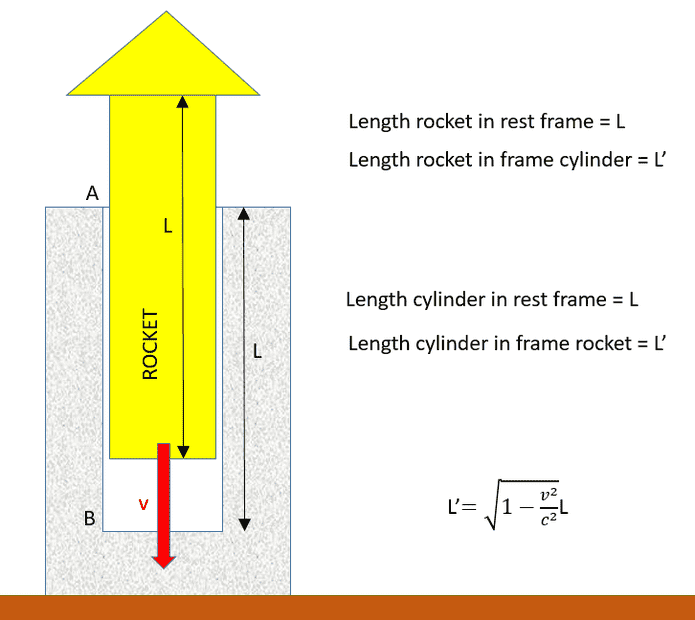
(1) What is it going to happen? Head damaged? Floor of cylinder damaged? Both damaged? Which part will be damaged first?

I think both will be damaged. From the point of view of an observer on the rocket the soil at B will be damaged first. From the point of view of an observer on the cylinder the head will be damaged first at A.

(2) Is it possible to start just in time the engine such that only the head of the rocket is destroyed or only the soil is destroyed?

What I want to know is that if for the observer on the rocket, the soil is damaged first, is it possible to program the engines of the rocket to accelerate such that damage to the head will be avoided. Is one engine enough? Or do I need multiple engines to get a distributed force?

(3) Is it necessary to include the concept of rigidity? Is it necessary to consider the rocket as made up of atoms that cannot transmit information infinitely fast or is it possible to solve it as a geometric problem?

 

[Ibix]

http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/bugrivet.html

 

[PeroK]

(1) What is it going to happen? Head damaged? Floor of cylinder damaged? Both damaged? Which part will be damaged first?

I think both will be damaged. From the point of view of an observer on the rocket the soil at B will be damaged first. From the point of view of an observer on the cylinder the head will be damaged first at A.

Yes, both will be damaged.

(2) Is it possible to start just in time the engine such that only the head of the rocket is destroyed or only the soil is destroyed?

What I want to know is that if for the observer on the rocket, the soil is damaged first, is it possible to program the engines of the rocket to accelerate such that damage to the head will be avoided. Is one engine enough? Or do I need multiple engines to get a distributed force?

Of course, the head of the rocket could detach and avoid the collision. But in both frames this would have to happen before it reaches the top of the cylinder.

(3) Is it necessary to include the concept of rigidity? Is it necessary to consider the rocket as made up of atoms that cannot transmit information infinitely fast or is it possible to solve it as a geometric problem?

Yes, definitely. An infinitely rigid object is impossible in SR.

 

[wnvl2]

Another question. Is it possible to make the rocket land in the cylinder without deformation according to special relativity? I was thinking to distribute engines all over the rocket such that all accelerations in the "frame of the rocket" (I am not sure that in this case "frame of the rocket" is the correct term because of the distributed acceleration) are distributed such that the length of the rocket is allways conserved in its own frame.

p.s. I am thinking about an adaptation of Bells paradox where the cords keep the same length in their frame.

 

[PeroK]

Another question. Is it possible to make the rocket land in the cylinder without deformation according to special relativity? I was thinking to distribute engines all over the rocket such that all accelerations in the "frame of the rocket" (I am not sure that in this case "frame of the rocket" is the correct term because of the distributed acceleration) are distributed such that the length of the rocket is allways conserved in its own frame.

That's easy to do conceptually. It (each atom) just has to decelerate at the right time. You may notice that as it decelerates, it will became less length contracted (in the cylinder frame). So, in that frame the acceleration is not uniformly synchronous across the length of the rocket.

In the rocket frame, however, it could maintain the same proper length. This is called Born Rigidity:

https://en.wikipedia.org/wiki/Born_rigidity

 

[wnvl2]

Ok, to do that I need one engine for each atom in principle.

To be sure, if I attach in that case a frame that 'comoves' with the bottom of the rocket (I can not call it an inertial frame), in that frame all atoms of the rocket are standing still. In the inertial frame attached to the cylinder all atoms of the rocket have a different acceleration and a different velocity?

 

[PAllen]

Ok, to do that I need one engine for each atom in principle.

To be sure, if I attach in that case a frame that 'comoves' with the bottom of the rocket (I can not call it an inertial frame), in that frame all atoms of the rocket are standing still. In the inertial frame attached to the cylinder all atoms of the rocket have a different acceleration and a different velocity?

Yes, if the rocked us accelerating or decelerating in a Born rigid manner, then an inertial frame will see each rocket 'atom' having different acceleration and velocity.

 

[jartsa]

Ok, to do that I need one engine for each atom in principle.

To be sure, if I attach in that case a frame that 'comoves' with the bottom of the rocket (I can not call it an inertial frame), in that frame all atoms of the rocket are standing still. In the inertial frame attached to the cylinder all atoms of the rocket have a different acceleration and a different velocity?

Well, if each atom just stops abruptly when at its final position, is there some problem with that?

If the speed is really high then that ssems to be the only way that the landing can happen .

 

[wnvl2]

No problem for me, but that implies that the rocket will deform. I just wanted confirmation that it is possible to stop the rocket in a way without deformation.

 

[PAllen]

No problem for me, but that implies that the rocket will deform. I just wanted confirmation that it is possible to stop the rocket in a way without deformation.

While there may be no way to achieve a Born rigid deceleration in practice, if it were achieved "somehow", there would be no stresses or strains or compression or tension within the rocket.

 

[jartsa]

No problem for me, but that implies that the rocket will deform. I just wanted confirmation that it is possible to stop the rocket in a way without deformation.

The underside of the head has to stop abruptly, in the cylinder frame, right? After stopping, the underside is in the frame of the cylinder, the cylinder and the underside observe the lower part of the very short rocket continue moving. This can be described as deforming, right?

There is no stress, because the nano-rockets cancel out any stress, as that's part of their job.

Atoms of solid matter are in a potential well, this keeps the solid matter solid. When a nano-rocket fires abruptly, it pulls its atom out of the potential well that the atom is sitting in, again without stress. This increases the potential energy inside the matter. This extra energy may destroy the landing pad. The rocket is safe, as the nano-rockets keep it stress free.

 

[PeroK]

When a nano-rocket fires abruptly, it pulls its atom out of the potential well that the atom is sitting in.

What sort of rocket can you attach to an individual atom?

 

[jartsa]

What sort of rocket can you attach to an individual atom?

I don't know. It's OP's idea. Post #6.

 

[PeroK]

I don't know. It's OP's idea. Post #6.

Well, no, it wasn't his idea to attach an engine to every atom. That was your suggestion.

 

[wnvl2]

Attaching a rocket to each atom was only a conceptual idea. I would approach it using one rocket for 1000000xxx atoms as an approximation to limit stresses.

 

[Nugatory]

In the inertial frame attached to the cylinder all atoms of the rocket have a different acceleration...

This might be a good time to mention the distinction between coordinate acceleration and proper acceleration. Proper acceleration is what an accelerometer measures - the difference between the path and object would follow if it were moving inertially, no applied force, no rocket attached - and is the same in all frames. Coordinate acceleration is the change in velocity over time; both of these quantities are frame-dependent and coordinate-dependent so coordinate acceleration also is.

The proper acceleration will be different for the different parts of an accelerating Born-rigid object, no frames involved.

 

[OscarCP]

In my opinion, in one special case, when the rocket touches first with the cone and both rocket and receiving cylinder are perfectly rigid bodies, this stops the rocket instantly, so now it fills the whole receiving cylinder, as it is stationary in the frame of this Earth-fixed cylinder and the special relativity effect ceases to make a difference in the length of rocket and receiving cylinder. That is, the cone touching the top of the receiving cylinder stops completely the rocket in the frame of the cylinder and both cone and bottom of the rocket touch the top and bottom, respectively, of the receiving cylinder at the same time.

Again, this is assuming the rocket and the receiving cylinder are perfectly rigid bodies, If they are not, I suspect we may need pages of equations to sort this one out.
The question, as posed, does not exclude both rocket and receiving cylinder being rigid, so it is OK to assume both are.

If the rocket is still decelerating, then it is in an accelerated frame and Special Relativity does not apply: this is now the province of General Relativity, or in this case of small velocities and accelerations, of its post-Newtonian mechanics approximation. And then that gets a bit more complicated

 

[Nugatory]

If the rocket is still decelerating, then it is in an accelerated frame and Special Relativity does not apply: this is now the province of General Relativity

This is a very common misconception; special relativity works just fine with accelerations. Googling for "Rindler coordinates" will find you one good example, and Bell's spaceship paradox is another.

General relativity is only needed in non-flat spacetimes where gravitational tidal effects are significant.

 

[Nugatory]

The question, as posed, does not exclude both rocket and receiving cylinder being rigid,

It does not, but that's just the trick of this paradox. The presenter is hoping that if they don't mention rigidity, someone will forget that there are no rigid objects in relativity.

 

[PeterDonis]

In my opinion, in one special case, when the rocket touches first with the cone and both rocket and receiving cylinder are perfectly rigid bodies, this stops the rocket instantly

Your opinion is incorrect. It takes a finite time for the effect of the rocket touching to propagate from one end of the rocket to the other (because internal forces within the rocket that propagate the effect cannot do so faster than light). So it is impossible for the rocket to stop "instantly". To put this another way, the finite propagation speed of internal forces in relativity means there are no such things as "perfectly rigid bodies" in relativity.

The question, as posed, does not exclude both rocket and receiving cylinder being rigid

It doesn't have to. Relativity does.

 

[OscarCP]

It does not, but that's just the trick of this paradox. The presenter is hoping that if they don't mention rigidity, someone will forget that there are no rigid objects in relativity.

Nugatory: There can be bodies that are perfectly rigid in their own frames -- in a purely geometric interpretation of the problem, with only the Lorentz-Fitzgerald contraction taken into account.
However, there is the question of the "stop" signal traveling from top to bottom taking a finite time, because it cannot travel faster than the speed of light, as PeterDonis has just reminded me. Thanks!.
OK. So the rocket stops entirely in the twinkling of an eye, and the rocket and the receiving cylinder, being now in the same frame and being of the same lengths, the bottom of one will coincide with that of the other.

The reply to the problem would be that the top stops first, then the bottom. But the bottom of the rocket does not "hit" that of the receiving cylinder, because to get to it, it must stop first ...

 

[Nugatory]

There can be bodies that are perfectly rigid in their own frames.

No, there cannot be.
You may be confusing yourself with that phrase “their own frame”, which is a common but inaccurate way of saying “that inertial frame in which all parts of the body in question are at rest”. But rigidity is about how a body moves when one part of it is displaced - and there is no inertial frame in which all parts of the body are at rest and some part of it is displaced.

The closest we can come to the classical notion of “perfectly rigid” is Born rigid motion, also worth googling for.

 

[Nugatory]

The reply to the problem would be that the top stops first, then the bottom. But the bottom of the rocket does not "hit" that of the receiving cylinder, because to get to it, it must stop first ...

No. The problem is most easily analyzed using the frame in which the rocket is at initially at rest because we don’t have to deal with the rigidity issues; and when we use that frame we see that the bottom of the rocket hits the bottom of the cylinder. But the result must be the same no matter what frame we use, so we don’t have to do the messy and error-prone calculations using the frame in which the Earth is at rest to know that if we do them right we’ll get the same result.

Note that in the rocket-at-rest frame the bottom of the rocket hits before the top, while in the earth-at-rest frame the top hits before the bottom. This is the relativity of simultaneity at work, and it is the key to almost all relativity paradoxes.

 

[OscarCP]

No. The problem is most easily analyzed using the frame in which the rocket is at initially at rest because we don’t have to deal with the rigidity issues; and when we use that frame we see that the bottom of the rocket hits the bottom of the cylinder. But the result must be the same no matter what frame we use, so we don’t have to do the messy and error-prone calculations using the frame in which the Earth is at rest to know that if we do them right we’ll get the same result.

Note that in the rocket-at-rest frame the bottom of the rocket hits before the top, while in the earth-at-rest frame the top hits before the bottom. This is the relativity of simultaneity at work, and it is the key to almost all relativity paradoxes.

Interesting problem, isn't it?

However, if the velocity of the descending rocket is small enough compared to that of light, and also to that of sound, I suspect -- and there is nothing in the formulation of the problem that says it cannot be so -- then by the time the "stop" signal from the cone gets to the bottom of the rocket body and this is completely stopped in the frame of the receiving cylinder, the rocket and this cylinder will be in the same inertial frame and simultaneously no longer moving relative to each other, and my previous conclusion does still apply, I think

 

[Nugatory]

and there is nothing in the formulation of the problem that says it cannot be so

Ah, but there is. As the problem is stated, the length contraction (of the cylinder or the rocket or both, depending on which frame we use to analyze the problem) is sufficient for the apparent paradox to arise.

More precisely, the two events “bottom of rocket reaches botttom of cylinder” and “top of rocket reaches top of cylinder” must be spacelike-separated because which happens first is different in the two frames. That places a lower bound on the relative speed (and it would be a good exercise to calculate it - use the frame in which the rocket is at rest, it’ll be easier).

 

[Halc]

What sort of rocket can you attach to an individual atom?

Think of it as thrust being applied to each atom individually from outside, such as in a rail gun. I guess it wouldn't really be a rocket then, just a rigid rod (stress free) with a cap at the end and variable force being externally applied everywhere.

The cap cannot 'stop' in negligible time. Only the rear can do that.

It was posed to me to figure out how long it might take to move a 100 light-year object a distance of one light-hour, sort of like a really long subway train starting and stopping. It took at least 55 days to do it without deformation of the object. The question of how to apply the thrust came up, but it is an engineering issue, not directly relevant to the question asked. Indeed, the thrust (even low-G acceleration) cannot come from one or a small number of places without deformation of the object.

 

[OscarCP]

Ah, but there is. As the problem is stated, the length contraction (of the cylinder or the rocket or both, depending on which frame we use to analyze the problem) is sufficient for the apparent paradox to arise.

More precisely, the two events “bottom of rocket reaches botttom of cylinder” and “top of rocket reaches top of cylinder” must be spacelike-separated because which happens first is different in the two frames. That places a lower bound on the relative speed (and it would be a good exercise to calculate it - use the frame in which the rocket is at rest, it’ll be easier).

Whatever happens, the final state and condition of the rocket/cylinder system, when both rocket and container cylinder are no longer moving relative to each other, should be the same regardless in which frame one describes the arrival of the rocket. This does not solve the apparent paradox right away, but I think is the right way to get to the solution, without the need of calculating anything.

The answer probably has to do with the fact that the rocket is in accelerating frame -- actually decelerating. For example, if the rocket velocity relative to the cylinder drops to zero exactly when, in its own frame, it touches the cylinder's bottom, then both rocket and cylinder are in the same frame and, consequently of the same length in it at that instant, and the rocket top and bottom touch the cylinder's top and bottom at the same time in the rocket frame and, therefore, in the cylinder's, as both are now the same.
The interesting question then is what happens if the rocket is still moving.

 

[PeterDonis]

If the rocket velocity relative to the cylinder drops to zero exactly when, in its own frame, it touches the cylinder's bottom

Again, this is impossible. The rocket's velocity cannot change instantaneously in all parts of the rocket. The force that stops the rocket can only propagate through the rocket at a finite speed.

You cannot possibly reason correctly about any problem if you start with false premises.

 

[PeterDonis]

The answer probably

No "probably" is required. The answer has already been given, earlier in this thread.

 

[OscarCP]

I think this is actually possible if one assumes the whole rocket, by whatever mechanism, is decelerating together, as when a rock thrown upwards slows down under gravity with all its parts slowing together. The way the question has been asked, it does not negates this possibility, because it says nothing against it.
But this is too cheap a way to get to an answer.
One thing I don't recall having been considered so far is that, assuming the rocket is in a gravity field, then so is the cylinder: each is in an accelerated frame, not an inertial one. I wonder what difference does this fact make here.