Requirements for pair production

[mark!]

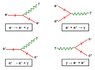
Pair production only occurs with high energetic photons (gamma rays rather than infrared rays, because a photon needs to have a higher energy than the sum of the rest mass energies of the electron and the positron).

Where (on Earth and/or in space) does this occur? And why don't ALL gamma rays produce e+ and e- particles, but some gamma rays evidently do? Are there environmental requirements?

 

[Orodruin]

A photon cannot spontaneously pair produce an electron-positron pair as that would violate the conservation of 4-momentum (i.e., energy and 3-momentum). You need some background that absorbs part of the momentum in order for pair production to be possible.

 

[mark!]

@Orodruin Quantum fluctuations ("borrowing" energy from the universe) are violating the law of conservation of energy (which doesn't automatically mean it can't occur), don't you agree?

Moreover, 4-momentum is a term from 'special relativity', which contradicts 'quantum physics' on so many more levels, so I'm not sure whether this comparison is applicable.

 

[Orodruin]

Quantum fluctuations ("borrowing" energy from the universe) are violating the law of conservation of energy (which doesn't automatically mean it can't occur), don't you agree?

No. In fact, what is violated by "virtual particles" is not energy or momentum conservation, but the dispersion relation of on-shell particles. Also, I suggest you read this.

Moreover, 4-momentum is a term from 'special relativity', which contradicts 'quantum physics' on so many more levels

This is just wrong. Besides, energy and momentum is conserved even in classical physics.

 

[vanhees71]

You need two photons, i.e., pair-production, which is the time-reversed process of pair annihilation, is usually understood as the reaction $\gamma+\gamma \rightarrow \mathrm{e}^+ + \mathrm{e}^-$. AFAIK it has not been observed yet, also from QED we are very sure it must happen.

A single photon cannot decay to a pair of massive particles at all, because you cannot satisfy energy-momentum conservation.

Last but not least, "virtual particles" are called "virtual", because they don't exist in Nature. It's just sloppy language for a formal expression from QFT perturbation theory. In Feynman diagrams its symbolized by internal lines, which stand for (time-ordered) propagators of the corresponding fields.

 

[weirdoguy]

Moreover, 4-momentum is a term from 'special relativity', which contradicts 'quantum physics' on so many more levels

It does not contradict relativistic quantum physics. Have you ever heard about quantum field theories? SR is built in most of them. You've mistaken SR with general relativity. Special relativity blends excelent with quantum theories.

 

[vanhees71]

To add, as soon as photons are involved it's relativistic (at least partially; of course you can treat massive particles in the non-relativistic approximation, as done in atomic and condensed-matter physics; photons themselves are of course as relativistic as anything can get!). The most successful theory ever, called the Standard Model of elementary-particle physics, is based on making quantum theory compatible with special relativity!

 

[mark!]

A single photon cannot decay to a pair of massive particles at all, because you cannot satisfy energy-momentum conservation.

If you need two photons instead of only one, in order for energy-momentum to be conserved, then why do I read on the 'pair production' Wikipedia page the following:

The energy of a photon can be converted into an electron-positron pair: γ → e− + e+

 

[vanhees71]

You have to read the complete text. In this case Wikipedia is not wrong (maybe a bit unfortunate in explaining it):

The photon must be near a nucleus in order to satisfy conservation of momentum, as an electron-positron pair producing in free space cannot both satisfy conservation of energy and momentum.[4] Because of this, when pair production occurs, the atomic nucleus receives some recoil. The reverse of this process is electron positron annihilation.

 

[mark!]

@vanhees71 You're mentioning the reverse process: electron–positron annihilation. Are there similar energy-momentum requirements for e- and e+ to form γ in the sun? There's no nucleus at the end (to receive some recoil), so how would you explain conservation of energy in this reverse process?

 

[vanhees71]

It's the same kinematics constraint. At tree level you have $\mathrm{e}^+ + \mathrm{e}^- \rightarrow \gamma + \gamma$ as the basic process.

Let's do the calculation to prove that $\mathrm{e}^+ + \mathrm{e}^- \rightarrow \gamma$ is impossible. Let $p_1$ and $p_2$ the four-momenta of the electron and positron in the initial and $q$ the four-momentum of the photon in the final state. We use natural units with $\hbar=c=1$ then the kinematical constraints read
$$p_1+p_2=q,$$
which is energy-momentum conservation for the process and
$$p_1^2=p_2^2=m^2, \quad q^2=0$$
where $m$ is the electron mass, and photons are massless. Now you have
$$(p_1+p_2)^2=p_1^2+p_2^2+2 p_1 \cdot p_2=2 (m^2 + p_1 \cdot p_2)=0.$$
Now you can go into the center of mass frame of the incoming electrons, i.e., you make
$$\vec{p}_1=-\vec{p}_2=\vec{p}_{\text{cm}},$$
and then you get
$$(p_1+p_2)^2=2 (m^2+E_{\text{cm}}^2+\vec{p}_{\text{cm}}^2)>0,$$
i.e., for no $\vec{p}_{\text{cm}}$ you can fullfil the onshell condition for the photon. Thus the process cannot happen.

 

[mark!]

That's weird, the proton-proton cycle has taught me that an electron annihilates with a positron to form one gamma ray. The image is kind of misleading, your explanation however is very clear!

 

[vanhees71]

Read the stuff careful! Nowhere in the entire Wikipedia article is written what you've claimed!

 

[mark!]

This image is incorrect and very misleading (I just found out). Nothing beats calculations ;)

 

[vanhees71]

Yes, you should always draw complete Feynman diagrams. In the case of pair creation in the sense meant here, it's $\gamma+A \rightarrow e^+ +e^- +A$, where $A$ stands for a nucleus. It's quasi-elastic scattering on a nucleus, i.e., the nucleus stays the same but takes the energy and momentum transfer as needed to get the energy-momentum balance right.

 

[mark!]

@vanhees71 Thanks a lot!

 

[mark!]

@vanhees71 Is it true that photons don't have number conservation? Then why, if I understand you correctly, aren't we able to therefore conclude that they're able to just (dis-)appear without the "help" of nucleus, and produce pairs?

To prove your point, you calculated that e+ + e- = gamma ray = impossible. I'm not able to understand all your calculations, but I believe you. So, if this is this case, could you therefore explain why this reaction seem te be happening in our sun (in the proton-proton chain this matter-antimatter-annihilation happens all the time). Or, if it's still not possible without a nucleus, how/where is this nucleus involved in the process?

I prefer an explanation without too much mathematical equations. I hope that's possible ;)

 

[Orodruin]

Then why, if I understand you correctly, aren't we able to therefore conclude that they're able to just (dis-)appear without the "help" of nucleus, and produce pairs?

Because they carry 4-momentum and 4-momentum is conserved.

 

[Nugatory]

@vanhees71 Is it true that photons don't have number conservation? Then why, if I understand you correctly, aren't we able to therefore conclude that it's able to just (dis-)appear without the "help" of nucleus, and produce pairs?

The problem with that reaction isn't that it changes the number of photons (which happens all the time), it is that it would violate at least one of energy conservation and momentum conservation. The momentum of a photon with a given energy is greater than the momentum of an electron-positron pair with the same energy so if the photon were to turn into two photons we'd end up with more energy or less momentum.

Could you therefore explain why this reaction seem te be happening in our sun (in the proton-proton chain this matter-antimatter-annihilation happens all the time). Or, if it's still not possible without a nucleus, how then is this nucleus involved in the process?

Are you asking about pair production or matter-antimatter annnihilation? The annihilation reaction for electrons is $e^++e^-\rightarrow\gamma+\gamma$ (two photons are created, not one, and no heavy nucleus is required) and similarly for other types of particle-antiparticle pairs. The pair production reaction is $\gamma+Z\rightarrow{e}^++e^-+Z$. The nucleus $Z$ appears unchanged by the reaction but in fact its momentum does change, just enough to make up for the difference between the momentum of the photon and the combined momentum of the electron and the positron.

 

[vanhees71]

@vanhees71 Is it true that photons don't have number conservation? Then why, if I understand you correctly, aren't we able to therefore conclude that they're able to just (dis-)appear without the "help" of nucleus, and produce pairs?

To prove your point, you calculated that e+ + e- = gamma ray = impossible. I'm not able to understand all your calculations, but I believe you. So, if this is this case, could you therefore explain why this reaction seem te be happening in our sun (in the proton-proton chain this matter-antimatter-annihilation happens all the time). Or, if it's still not possible without a nucleus, how/where is this nucleus involved in the process?

I prefer an explanation without too much mathematical equations. I hope that's possible ;)

As has been already explained by @Orodruin and @Nugatory, indeed photon number is not conserved. In relativistic physics in general numbers of particles are not conserved, but only charge-like quantities (electric charge, baryon number, strangeness, etc., and approximately isospin as far as the electromagnetic and strong interaction is concerned). The reason is that in order to have a description as a local relativistic quantum-field theory (which is the so far only (very) successful kind of relativistic quantum theory disovered) you necessarily have to introduce for each particle also an antiparticle. You can always find a possibility to make the particles and antiparticles the same (such particles are called "strictly neutral"). The photon is an example for a strictly neutral particle.

All conservation laws are related to symmetries since any conserved quantity in a Hamiltonian system generates the corresponding symmetry operations via a Poisson bracket (one of Noether's famous theorems). In the case of the charge conservation rules of the standard model the symmetry is the symmetry of the fields' equations of motion under multiplication by a global (i.e., space-time independent) phase factor, realizing the symmetry group U(1) or more complicated matrix multiplications of multi-component fields, where the matrices build another group like SU(N) or SO(N) etc.

Of course, there are still the conservation laws from the fundamental symmetries of special relativistic spacetime, which is ruled by the proper orthochronous Poincare group, which is built by translations in space and time (homogeneity of space and time), rotations of space (isotropy of space), and Lorentz boosts (special principle of relativity). The corresponding 10 conserved quantities are energy (time translations), momentum (spatial translations), angular momentum (spatial rotations), and center of momentum (boosts).

So for pair creation from the point of view of charge conservation in the standard model you could well make an electron-positron pair (electric charge and total lepton number 0) to a single photon, but as we have seen above, that's not compatible with energy-momentum conservation, and thus this process does not happen in nature (at least as far as the standard model is telling us, and as far as empirical evidence so far confirms). What can happen according to all conservation laws is that an electron-positron pair annihilates to two photons, and that has been observed for a long time (I don't know the history by hard), including the correct quantitative prediction of the corresponding cross section.