Understanding Scattered Radiation in Photon Beams

[eneacasucci]

TL;DR Summary

scattered radiation of photons when passing through a material

Consider a source emitting a beam of photons. These photons pass through x thickness of material. The attenuation coefficient of the beam \mu is known.
We can write this formula

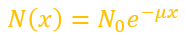
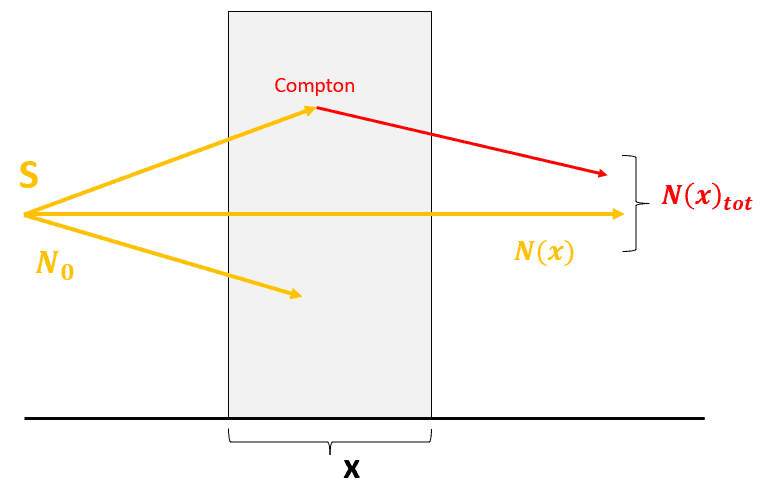
If I'm not wrong, this formula tells us the number of photons that passed through the material of thickness x without interacting with it (

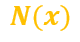), but it does not tell us the "real" total number of photons that we should expect to see beyond this material (

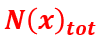) given by the sum of the first ones and the "scattered radiation".
My question is about what do we mean with "scattered radiation"?.
This is what I think about: "scattered radiation" are the photons resulting from the interaction of the primary beam with matter, that can happen in these ways:
1)photoelectric effect: with characteristic x-ray emission
2)Compton effect: in which the original photon loses energy, which is transferred to an electron
3)pair production: in which additional photons may be emitted if positron-electron annihilation occurs
4)coherent scattering: photon undergoes deflection but does not lose energy

Are these photons (1,2,3,4) the ones constituting the so-called "scattered radiation"? is there something else?P.S. To get a correct estimate of the photons passing through the material, thus also considering scattered photons, I should add a correction term, how is it estimated?

 

[malawi_glenn]

There is also possibility of no interaction at all, right?

 

[eneacasucci]

There is also possibility of no interaction at all, right?

Yes I think so, as I've written, the number of photons that pass through the material without interacting should be given by this formula

 

[malawi_glenn]

That formula does not take into account "rescattering" becuase it is assumed that the in comming radiation is monoenergetic. Keep in mind that $\mu$ depends on the photon energy. For a more detailed treatment you need to perform simulations use e.g. Geant4 software

 

[Nugatory]

@eneacasucci, could you please use Latex for your equations instead of embedding images? For example $N(x)=N_0e^{-\mu x}$ - there’s a Latex guide linked right below where you type posts/replies.

 

[eneacasucci]

That formula does not take into account "rescattering" becuase it is assumed that the in comming radiation is monoenergetic. Keep in mind that $\mu$ depends on the photon energy. For a more detailed treatment you need to perform simulations use e.g. Geant4 software

yes sure, $\mu$ depends on the energy of the photon.
Could I ask if it is possible to have an answer for the green questions in the original post? :) thank you so much for your time

 

[eneacasucci]

@eneacasucci, could you please use Latex for your equations instead of embedding images? For example $N(x)=N_0e^{-\mu x}$ - there’s a Latex guide linked right below where you type posts/replies.

Unfortunately I can't edit my original post but I'll try to write everything in latex in future messages and posts, sorry

 

[hutchphd]

Yes I think so, as I've written, the number of photons that pass through the material without interacting should be given by this formula

This follows from assuming that any "scattering" removes the particle from the incident beam, never to be seen again. This is often a good approximation for open geometries and collimated beams. Also it is very easy to apply.
Particles being returned to the beam after repeat scattering are rare although some devices (lasers for instance) rely on this effect , so you need to understand the system. These problems are typically much more difficult to calculate.

 

[Nugatory]

Unfortunately I can't edit my original post but I'll try to write everything in latex in future messages and posts, sorry

That's good enough, no problem.