- #1
mklein
- 43
- 0
Dear physics forums
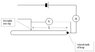
I am an A-level physics teacher and I have built, admittedly, a VERY simple circuit. The problem is that I cannot explain its behaviour. It involves a metre long wire, twisted at the ends to form a loop, and incorporated into a circuit as shown below: (or attached)
http://mpklein.co.uk/loop_circuit.jpg
What I cannot understand is that as I move the slider to the right, the voltage over the length "L" decreases and the total current drawn from the power-pack increases.
Is it not true that the circuit could effectively be redrawn as a parallel circuit? I have always taught in lessons that the voltage over any branch in a parallel circuit remains the same as the supply? In this parallel circuit I would expect lengthening one branch to reduce the length of the other. Therefore I would expect different currents through the branches e.g. if the top branch is shorter than the bottom, then I would expect a larger current through the top branch and smaller current through the bottom. But I would expect these currents to add up to some total which stays the same. So I would have expected my ammeter reading to stay the same!
I have built and tested the circuit yet it continues to confuse me. Please help as I am feeling very useless and not worthy of teaching at A-level !
Many thanks
Matt Klein
I am an A-level physics teacher and I have built, admittedly, a VERY simple circuit. The problem is that I cannot explain its behaviour. It involves a metre long wire, twisted at the ends to form a loop, and incorporated into a circuit as shown below: (or attached)
http://mpklein.co.uk/loop_circuit.jpg
What I cannot understand is that as I move the slider to the right, the voltage over the length "L" decreases and the total current drawn from the power-pack increases.
Is it not true that the circuit could effectively be redrawn as a parallel circuit? I have always taught in lessons that the voltage over any branch in a parallel circuit remains the same as the supply? In this parallel circuit I would expect lengthening one branch to reduce the length of the other. Therefore I would expect different currents through the branches e.g. if the top branch is shorter than the bottom, then I would expect a larger current through the top branch and smaller current through the bottom. But I would expect these currents to add up to some total which stays the same. So I would have expected my ammeter reading to stay the same!
I have built and tested the circuit yet it continues to confuse me. Please help as I am feeling very useless and not worthy of teaching at A-level !
Many thanks
Matt Klein