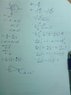Resistance of a sphere and cone

[lee_chongeu]

Lets assume we have a resistor material, with a perfect solid spherical shape and no defect, we connect it from south pole to north pole, by using the general formula of R=(rho)L/A where rho is the resistivity and L is the length of the resistor, and A is the cross sectional area. I found that i cannot integrate it, because i get a Log negative. I realize that the problem is at the point of contact between the wire and the spherical resistor's cross sectional area is close to zero.

Those are my question:
i) How to solve such conflict?
ii) How to integrate such resistor if i connect the wire 90 degree instead of pole to pole(180 degrees). What is the L length of the resistor? will it be the circumference of the sphere?
iii) I found the same problem occur when i change the shape to cone shape.

I've enclose my working

 

[John Creighto]

What happened to the squaring operation in your denominator?

 

[lee_chongeu]

There is nothing wrong wat?

 

[sstewari]

U have taken limits of integration as -r to +r. That u have to do if u start integrating from the center in which case R-L will become L. For ur integration, take limits as 0 to 2r. But even then the resistance will be infinite after integration. U can only find the resistance of a sphere or a cone between two limits say a and b not between 0 to 2r. Ur method is correct but the statement of question is wrong.

 

[cabraham]

The problem is that of singularities. The resistance is literally infinite. At the top or bottom of the sphere, where r = +/-R, or at the vertex of the cone, there is conductivity at only a point, the tangent point. A point has zero cross sectional area, hence infinite resistance. If the integration is evaluated from zero (center) to less than +R or -R, say +/- 1.9*R, then there is an area which is non-zero at the surface. In order to have finite resistance, the surfaces at each end must have non-zero area. A curved surface with one tangent point conducting will give infinite resistance. Does this help?

Claude