disclaimer
- 25
- 0
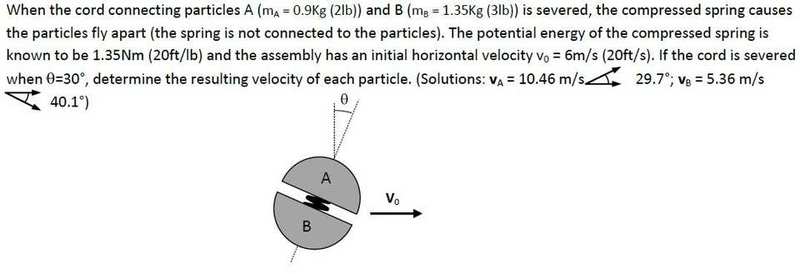
[solved] resulting velocity of 2 particles
conservation of momentum
m_Av_A'=m_Bv_B'
v_A'=\frac{m_B}{m_A}v_B'
conservation of energy
V=\frac{1}{2}m_A(v_A')^2+\frac{1}{2}m_B(v_B')^2=\frac{1}{2}m_A\left(\frac{m_B}{m_A}v_B'\right)^2+\frac{1}{2}m_B(v_B')^2
v_B'=\sqrt{\frac{2m_AV}{m_B(m_A+m_B)}}
m_A=0.9Kg
m_B=1.35Kg
V=1.35Nm
v_B'=\sqrt{\frac{2\cdot0.9\cdot1.35}{1.35(0.9+1.35)}}=\sqrt{0.8}\approx{0.8944[m/s]}
v_A'=\frac{1.35}{0.9}\cdot0.8944=1.3416[m/s]
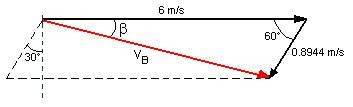
from the law of cosines
v_B=\sqrt{6^2+0.8944^2-2\cdot6\cdot0.8944\cdot\cos{60^o}}\approx5.607[m/s]
from the law of sines
\sin{\beta}=\frac{\sin{60^o}\cdot0.8944}{5.607}\approx0.1381
\beta\approx7.94^o
As you can see that result is totally different from the solution given by my teacher. I also get different results for the other velocity. So either my calculations are incorrect or my teacher gave us wrong results. I'll be grateful for any help, thank you.
Homework Statement
Homework Equations
conservation of momentum
m_Av_A'=m_Bv_B'
v_A'=\frac{m_B}{m_A}v_B'
conservation of energy
V=\frac{1}{2}m_A(v_A')^2+\frac{1}{2}m_B(v_B')^2=\frac{1}{2}m_A\left(\frac{m_B}{m_A}v_B'\right)^2+\frac{1}{2}m_B(v_B')^2
v_B'=\sqrt{\frac{2m_AV}{m_B(m_A+m_B)}}
The Attempt at a Solution
m_A=0.9Kg
m_B=1.35Kg
V=1.35Nm
v_B'=\sqrt{\frac{2\cdot0.9\cdot1.35}{1.35(0.9+1.35)}}=\sqrt{0.8}\approx{0.8944[m/s]}
v_A'=\frac{1.35}{0.9}\cdot0.8944=1.3416[m/s]
from the law of cosines
v_B=\sqrt{6^2+0.8944^2-2\cdot6\cdot0.8944\cdot\cos{60^o}}\approx5.607[m/s]
from the law of sines
\sin{\beta}=\frac{\sin{60^o}\cdot0.8944}{5.607}\approx0.1381
\beta\approx7.94^o
As you can see that result is totally different from the solution given by my teacher. I also get different results for the other velocity. So either my calculations are incorrect or my teacher gave us wrong results. I'll be grateful for any help, thank you.
Last edited: