Jacob White
- 55
- 12
So we know that every reversible engine working between the same temperatures will have the same efficiency(the same as Carnot engine). So let's consider for example reversible Otto cycle. So as you can see on the picture it is operating between ##T_1## and ##T_3##, so I was thinking that it should have efficiency ##f = 1 - \frac {T_1} {T_3}## Below there is a derivation assuming reversibility(Indeed it is reversible there is no entropy increase), however we don't get Carnot but: ##f = 1 - \frac {T_1} {T_2}## which is lower. How is it possible?
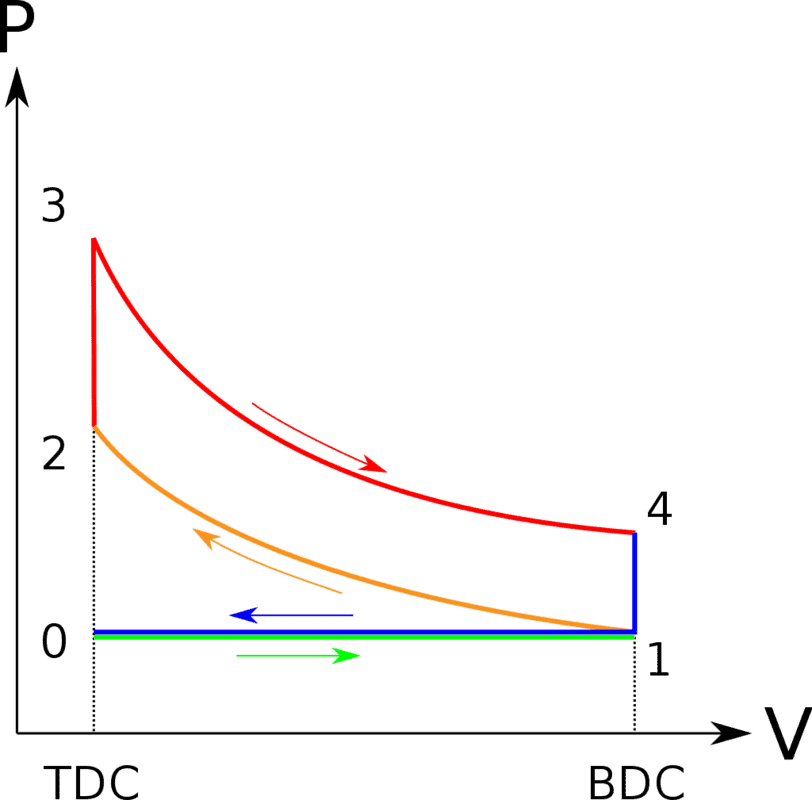 https://en.wikipedia.org/wiki/Otto_cycle
https://en.wikipedia.org/wiki/Otto_cycle
Last edited by a moderator: