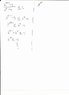Astrum
- 269
- 5
Homework Statement
\frac{2^{x+1}-3}{2^{x}-4}\leq1
Homework Equations
The Attempt at a Solution
When I go through it, I keep getting 2^{x}\leq-1
I don't think the answer is suppose to be complex... let me show you my work in a file.
It's extremely embarrassing that I don't remember this. Makes me feel pretty stupid...